Electric Forces and Electric Fields

Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations

Student Learning Objectives

To become familiar with basic electric phenomena.
To learn the charge model and use it to explain basic electric phenomena.
To understand polarization and the attraction between neutral and charged objects.
To understand and use Coulomb’s law for point charges.
To recognize and use the principle of superposition for electric forces.
To begin the process of understanding the field model and the concept of a field.
To learn the electric field of a point charge.
To use the principle of superposition to calculate the electric field of multiple charges and of continuous distributions of charge.
To learn the electric field of common charge distributions.
To learn the electric field of a parallel-plate capacitor and some of its applications.
To study the motion of charged particles and dipoles in simple electric fields.
To calculate forces and torques on charges in electric fields.

Lessons / Lecture Notes

The Physics Classroom (conceptual)

Electrostatics

PY106 Notes from Boston University (algebra-based):

Physics 2B notes from Dr. Bobby W.S. Lau (algebra-based)

HyperPhysics (calculus-based)

Physics 4B notes from Dr. Bobby W.S. Lau (calculus-based)

Important Equations (for algebra-based Physics)



word	pdf

Example Problems

Example Problems for algebra-based physics (from College Physics 2^nd Edition by Knight, Jones, and Field):

Example Problems (Electric Fields and Forces)
Solutions to Example Problems (Electric Fields and Forces)

Example Problems for calculus-based physics (from Fundamentals of Physics 9th Edition by Halliday, Resnick, and Walker):

Example Problems (Electric Charge and Forces) | Example Problems (Electric Field)
Solutions to Example Problems (Electric Charge and Forces) | Solutions to Example Problems (Electric Field)

Applets and Animations

Coulomb's Law		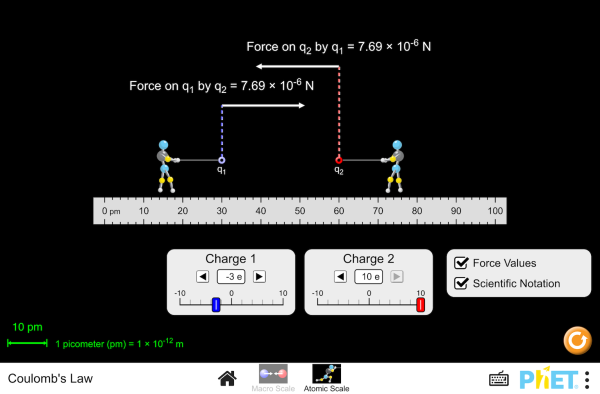Visualize the electrostatic force that two charges exert on each other. Observe how changing the sign and magnitude of the charges and the distance between them affects the electrostatic force.
Coulomb Interaction		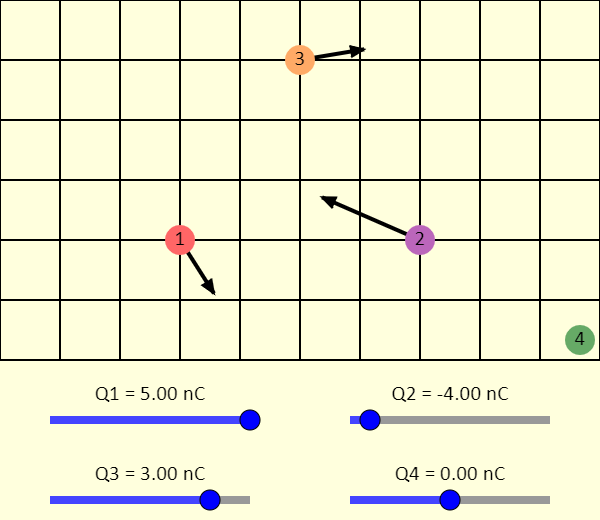In this simulation, you can explore the force between charged particles. You can drag the particles around the screen to change their positions. If you only want two or three of them, just set the charge on one or two of the particles to zero. You can display (or not) an arrow representing the net force being applied to each particle. You can also use the checkboxes to display the individual forces being applied to the particles by the other particles.
Coulomb Interaction		This is like the previous simulation, but this one shows the time evolution of the system. You can get some very interesting patterns, especially if you set the sliders so that two of the particles have a positive charge and two have a negative charge. What are some things that you notice? If two of the particles get into a death spiral, what can you change to get them out? Note that the simulation slows down by a factor of 10 when two particles get very close together. Even then, the physics may not be exactly right - it's hard to handle infinities well!
Coulomb's Law: Force vs. Position		In this simulation, you can investigate the force exerted by one charged particle on another, and how that force varies with the distance between the particles. The graph shows the force exerted on the movable charge, which is the one on the right. A force to the right on the movable charge is shown as positive on the graph; a force to the left on the movable charge is shown as negative
Electroscope		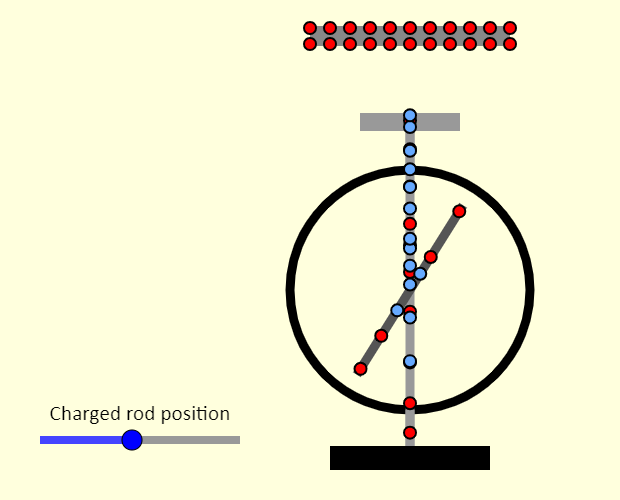Note that the electroscope here is always neutral, even at the beginning. If you bring the insulating charged rod closer to the electroscope, you'll be able to see that the electrons (in blue) and the positive charges (red) on the electroscope cancel one another out. When you bring the rod closer to the electroscope, the electroscope acts like it is charged even though it isn't. The electroscope becomes polarized. If the rod has a positive charge, electrons in the electroscope are attracted toward the rod and therefore the electrons move toward the top plate of the electroscope, leaving a net positive charge on and near the needle, which deflects. If, instead, the rod has a negative charge, electrons in the top plate of the electroscope are repelled by the electrons on the rod. The electrons on the electroscope move toward the needle, which then deflects. Moving the rod away reverses the movement of the electrons, so the needle deflects less.

Charges and Fields		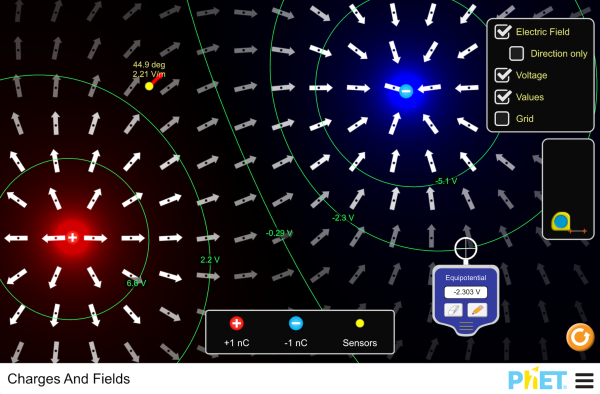Arrange positive and negative charges in space and view the resulting electric field and electrostatic potential. Plot equipotential lines and discover their relationship to the electric field. Create models of dipoles, capacitors, and more!
Electric Fields		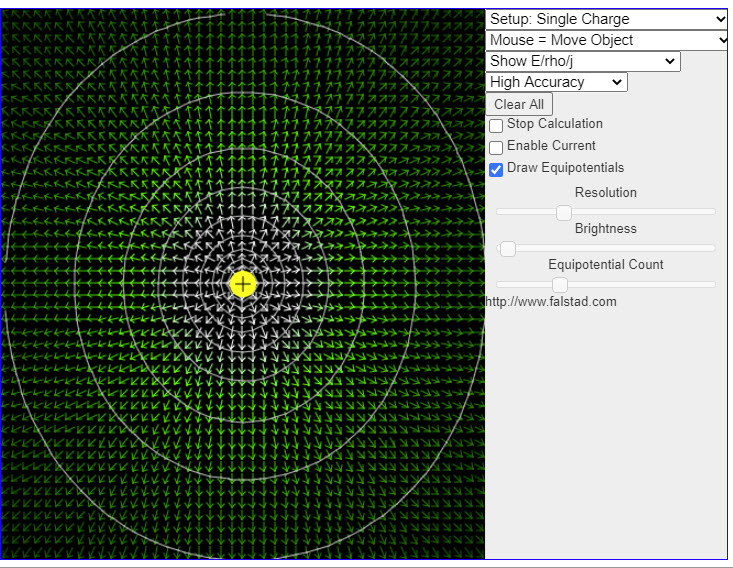This java applet demonstrates electrostatics and static current distributions in two dimensions. When the applet starts up you will see the electric field of a single positive charge. The charge can be dragged around the screen with the mouse. Go through the items in the Setup popup (located in the upper right corner) to view some interesting. pre-defined experiments. If you have a fast computer, you may want to set the Accuracy popup to "High Accuracy" to get better results.
Electric Field		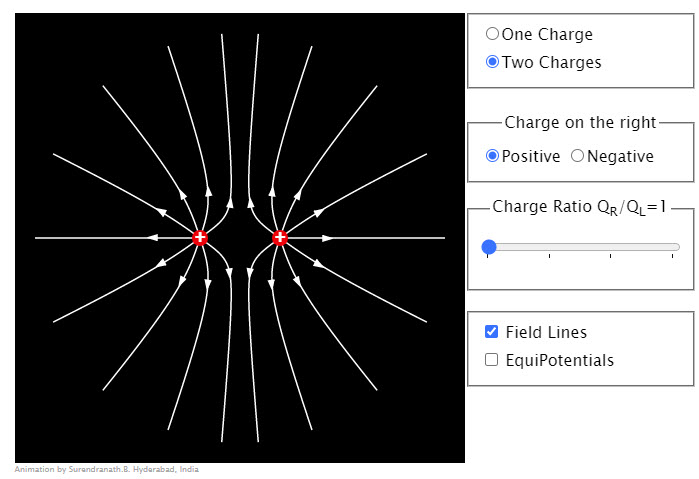Animation shows electric field lines due to charges. Initially the two charges are equal and equal number of lines of force are drawn from them. The ratio of charges can be varied by increasing the charge on the right. The number of field lines from the charge on the right increase proportionately. The sign of the charge on the right can also be changed. Both equipotentials and field lines can be observed by checking the corresponding boxes. The adjacent equipotentials differ in potentials by equal amounts. It might help to uncheck the field lines checkbox while observing the equipotentials. When charges are equal left/right clicking increases/decreases the distance between the charges.
Electric Fields		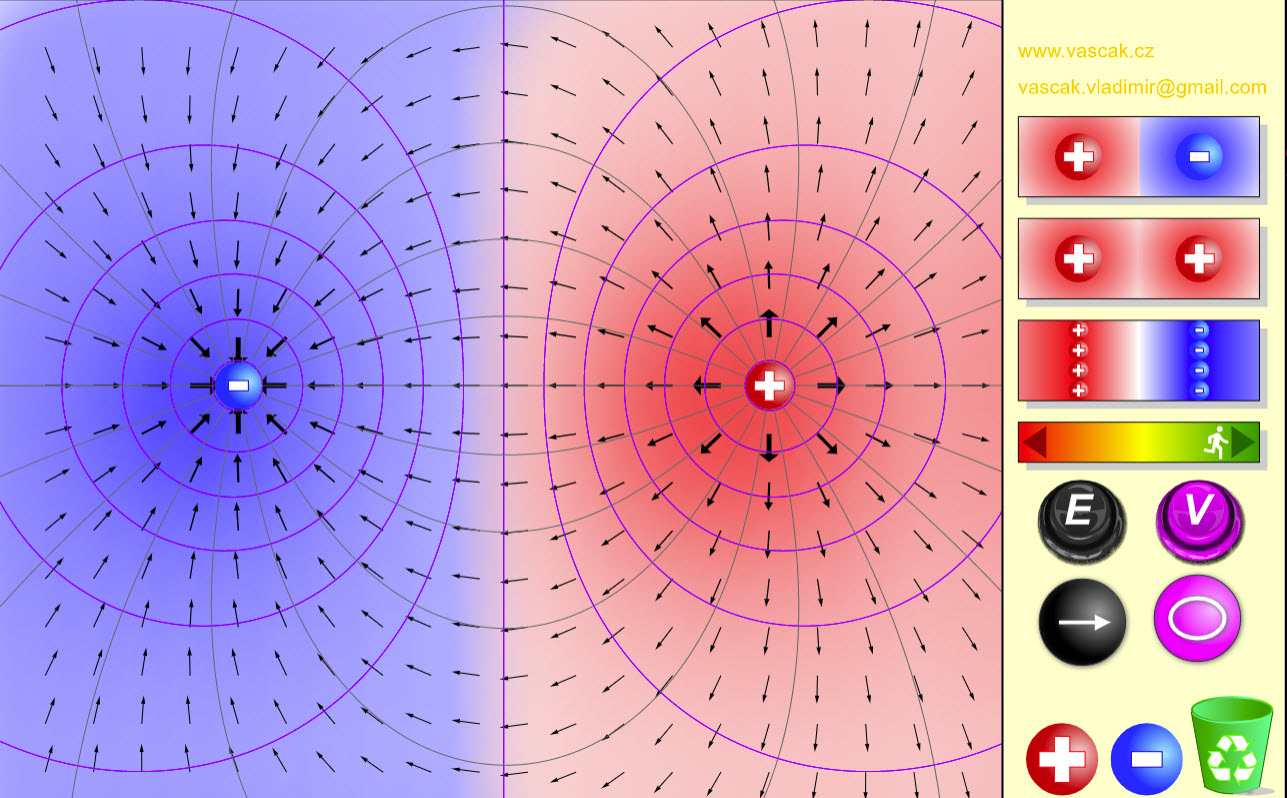Very nice animation showing the electric fields from different charge sources.
Electric Fields in Two DImensions		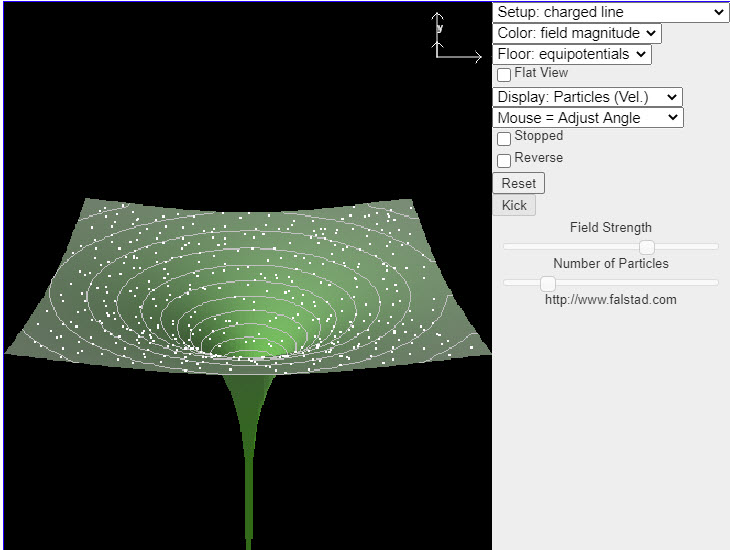This java applet displays the electric field in various situations. You may select one of many fields from the Setup menu in the upper right. The applet shows the potential surface of the field, with particles following the field vectors. You may click and drag with the mouse to rotate the view. Also some of the field selections have parameters which may be adjusted.
Electric Fields in Three DImensions		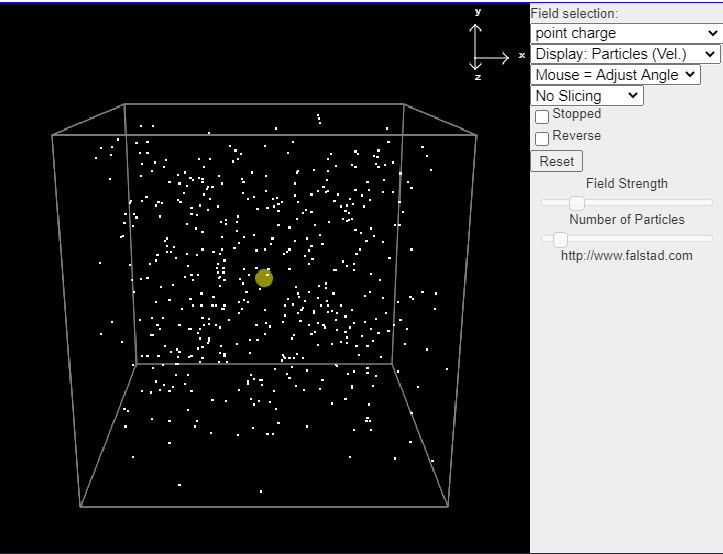This java applet is an electrostatics demonstration which displays the electric field in a number of situations. You can select from a number of fields and see how particles move in the field if it is treated as either a velocity field (where the particles move along the field lines) or an actual force field (where the particles move as if they were charged particles). This helps you visualize the field. The menu in the upper right has a variety of different fields to choose from.
Electric Field of Dreams		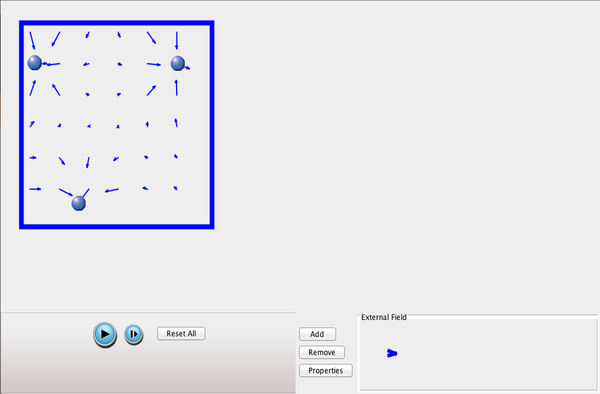Play ball! Add charges to the Field of Dreams and see how they react to the electric field. Turn on a background electric field and adjust the direction and magnitude. (Kevin Costner not included).
Electric Field Hockey		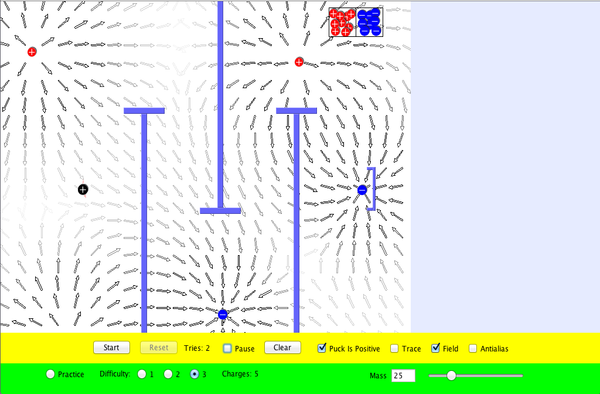Play hockey with electric charges. Place charges on the ice, then hit start to try to get the puck in the goal. View the electric field. Trace the puck's motion. Make the game harder by placing walls in front of the goal. This is a clone of the popular simulation of the same name marketed by Physics Academic Software and written by Prof. Ruth Chabay of the Dept of Physics at North Carolina State University.
Balloons and Static Electricity		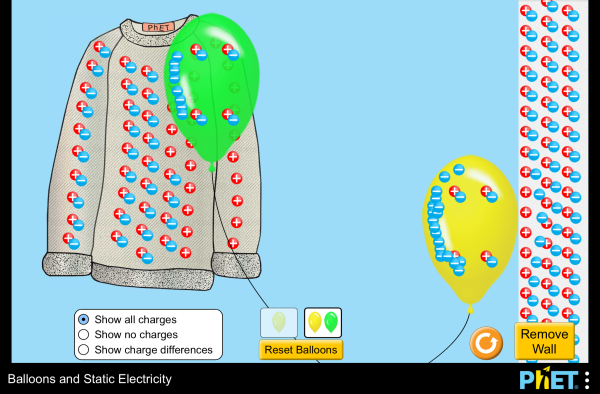Grab a balloon to explore concepts of static electricity such as charge transfer, attraction, repulsion, and induced charge.
John Travoltage		Play with John’s foot and arm to explore when he gets a zap!
Van De Graff Generator		Very cool applet showing a Van De Graff genertaor and various set-ups that you can implement.
Puzzle - Determine the Charge		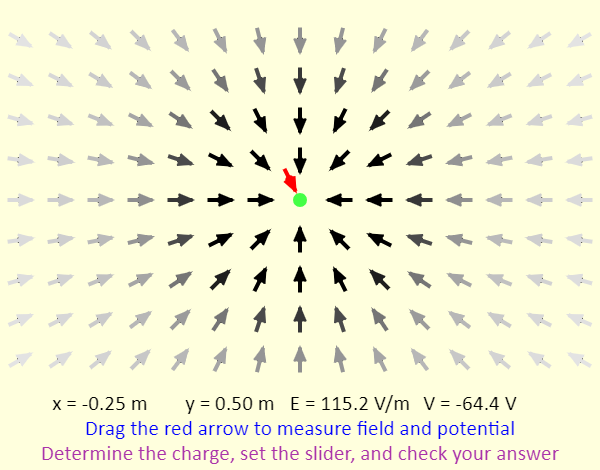In this simulation, the charged particle (in green) is randomly assigned a sign and a magnitude that is either 1, 2, 3, 4, or 5 nC. Your goal is to determine the charge - when you have figured out what it is, set the charge slider to that value and check your answer. to help you determine the charge, the field vector pattern near the charge is shown. There is also an electric field sensor (in red) that you can click-and-drag, moving it around the screen to sense both the electric field and the electric potential. The readouts of the position, field, and potential are at the bottom.
Charge in Electric Field		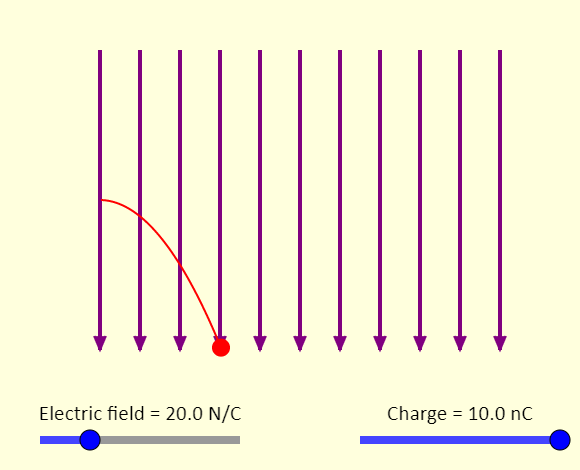This is a simulation of a charged particle being launched horizontally into a uniform electric field that is directed down. The sliders allow you to adjust the strength of the electric field as well as the charge on the particle. Note that gravity is neglected - we assume the gravitational force is negligible for all the situations shown. Explore the simulation - what changes when the strength of the electric field is changed? What changes when the particle's charge is adjusted?
Charged Ball on String in Electric Field		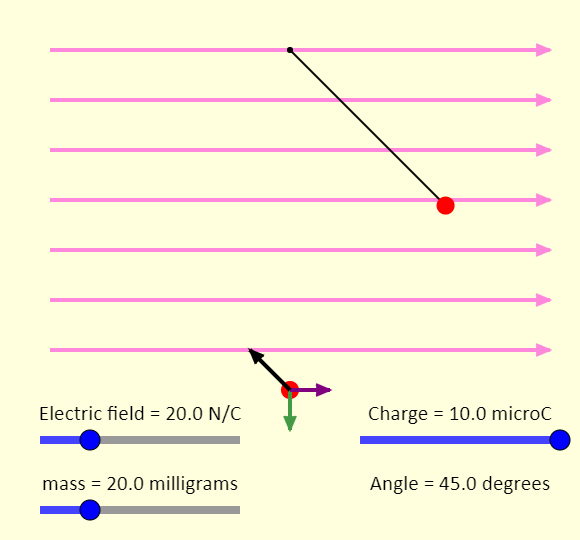This is a simulation showing the equilibrium position of a charged ball on a string. The sliders allow you to adjust the strength of the electric field (shown with the purple arrows), the charge of the particle, and the mass of the particle. The gravitational field is a constant 10 N/kg directed down. Explore the simulation - given the limitations set by the sliders, what is the maximum angle that can be achieved? How close to 0 degrees can you get? Also, can you identify each of the forces on the free-body diagram?
Electric Field on the Axis of a Ring		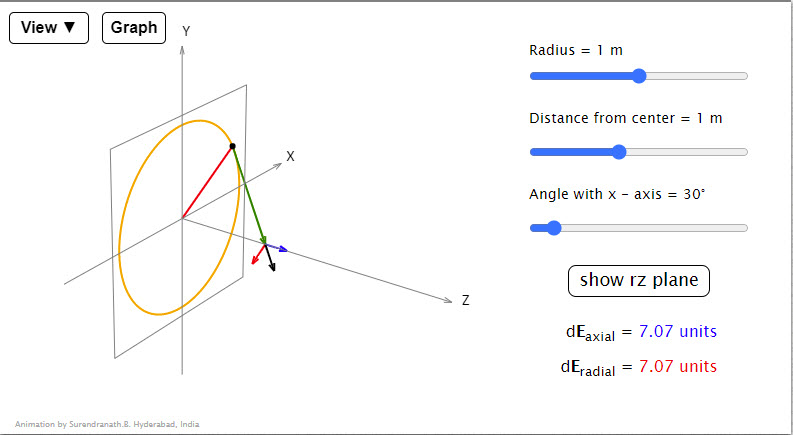Animation shows the electric field vector at a point on the axis of the ring due to a small charged element of a ring. The black dot is the dQ element, the green vector the radius vector r of the point on the axis relative to the dQ element and the black vector E is the electric field vector due to the element.
E,V Graphs		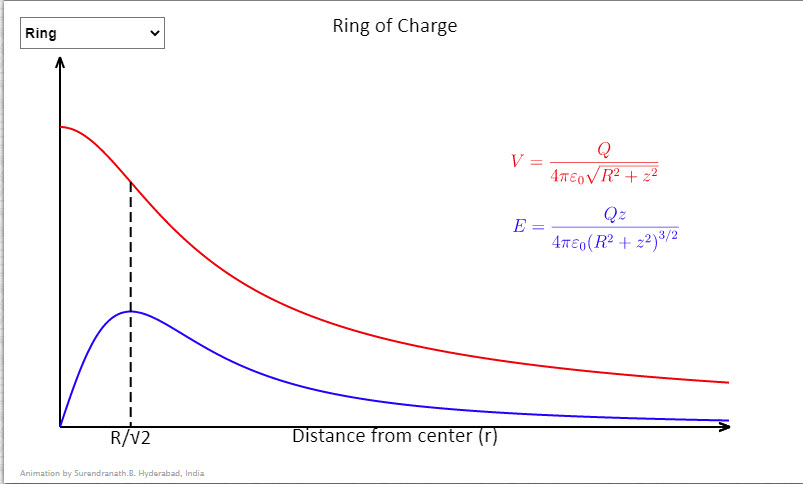Some useful graphs showing variation of potential and field strengths with distance. In the case of the shell charge on the shell is assumed constant and in case of the sphere charge density is assumed constant. In case of concentric shells the charge on the outer shell is double the charge on the inner shell. Radius of the shell/sphere/inner shell can be decreased/increased by taps on left/right halves of the graph.
Puzzle - Determine the Charges		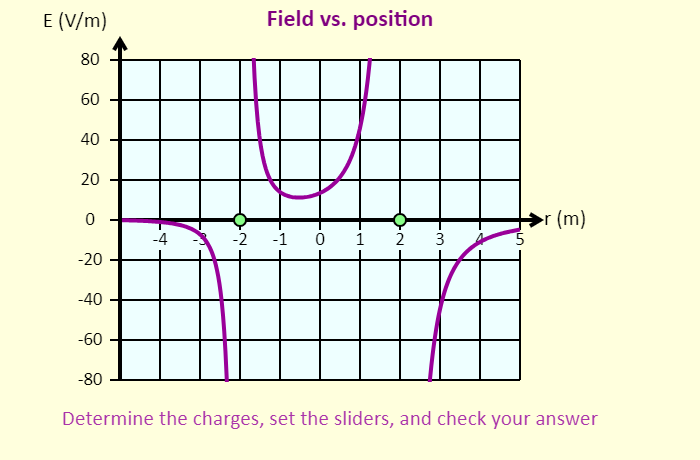In this simulation, the two charged particles (in green) are each randomly assigned a sign and a magnitude that is either 1, 2, 3, 4, or 5 nC. Your goal is to determine their charges, with the help of the graphs - when you have figured out what they are, set the charge sliders to those values and check your answer. You can click-and-drag the particles to move them left or right. The particle on the left is confined to the region to the left of the origin; the particle on the right is confined to the region to the right of the origin. In this simulation, you can see the graph of the electric field on the x-axis as a function of position, as well as the electric potential on the x-axis as a function of position. On the graph, the electric field is shown as positive if the net field at that position is directed to the right, and the field is shown as negative if the field is directed left. Using the sliders, you can adjust the charges of the particles.
Microwaves		How do microwaves heat up your coffee? Adjust the frequency and amplitude of microwaves. Watch water molecules rotating and bouncing around. View the microwave field as a wave, a single line of vectors, or the entire field.