Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations
Student Learning Objectives
Lessons / Lecture Notes
The Physics Classroom (conceptual)
PY105 Notes from Boston University (algebra-based):
Physics 2A notes from Dr. Bobby W.S. Lau (algebra-based)
HyperPhysics (calculus-based)
Physics 4A notes from Dr. Bobby W.S. Lau (calculus-based)
Important Equations (for algebra-based Physics)
Example Problems
Example Problems for algebra-based physics (from College Physics 2nd Edition by Knight, Jones, and Field):
Example Problems (Motion in One-Dimension)
Solutions to Example Problems (Motion in One Dimension)
Example Problems for calculus-based physics (from Physics for Scientists and Engineers 4th Edition by Knight):
Example Problems (Kinematics in One Dimension)
Solutions to Example Problems (Kinematics in One Dimension)
Applets and Animations
| Comparing Motion Diagrams | 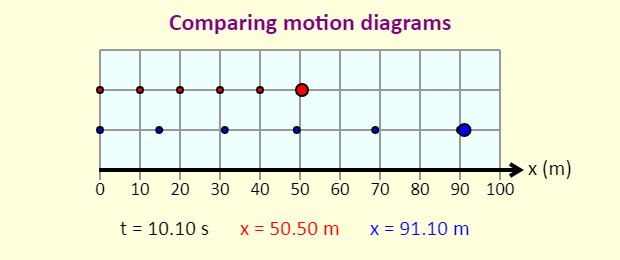 |
This useful animation allows you to compare the motion diagrams for two different sets of initial conditions. |
| Motion with Constant Acceleration | 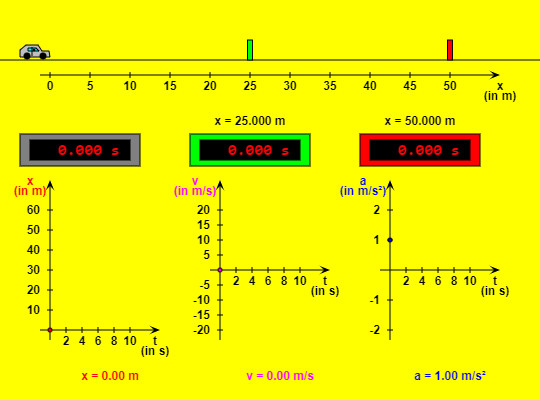 |
This HTML5 app shows a car moving with constant acceleration. The green control panel contains text fields where you can vary the values of initial position, initial velocity and acceleration (don't forget to press the "Enter" key!). By using the buttons at the top right you can bring the car back to its initial position or stop and resume the simulation. If you choose the option "Slow motion", the movement will be ten times slower. Three digital clocks indicate the elapsed time since the start. As soon as the car has reached the green or red barrier with its front bumper, the corresponding clock will stop. Both barriers can be dragged left or right. Three diagrams illustrate the motion of the vehicle: Position x versus time t, Velocity v versus time t, and Acceleration a versus time t |
| Constant Velocity vs. Constant Acceleration | 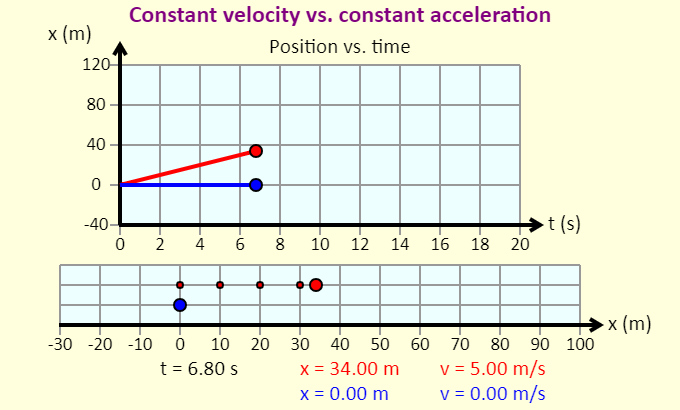 |
An excellent applet showing 1-dimensional kinematics of a body undergoing constant velocity and constant acceleration. The applet plots both the position versus time graph as well as the motion diagram. |
| Choose a Graph to Match | This awesome simulation shows 10 different graphs that you can try and match by adjusting the initial position, velocity, and constant acceleration. | |
| One-Dimensional Kinematics |
This applet shows position, velocity, and acceleration graphs for 10 different scenarios. |
|
| Maze Game | 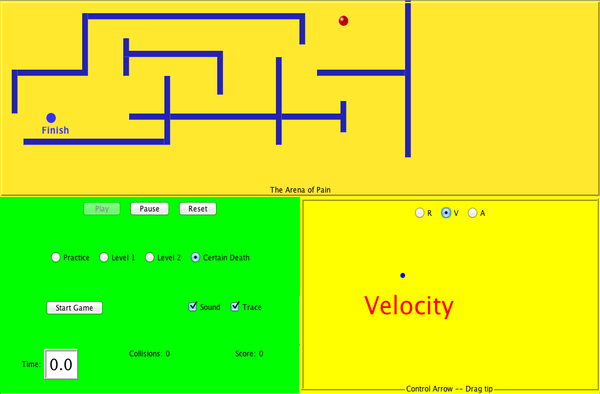 |
Learn about position, velocity, and acceleration in the "Arena of Pain". Use the green arrow to move the ball. Add more walls to the arena to make the game more difficult. Try to make a goal as fast as you can. |
| The Moving Man | 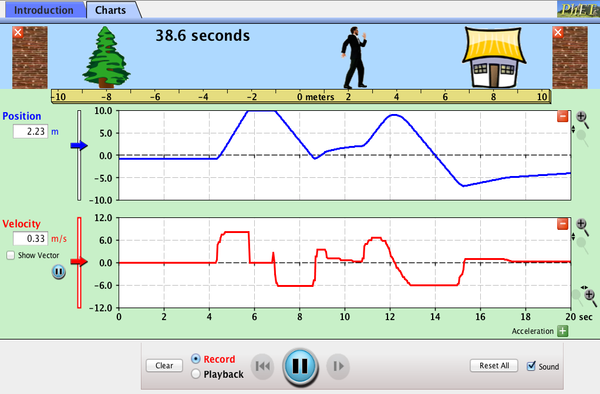 |
Learn about position, velocity, and acceleration graphs. Move the little man back and forth with the mouse and plot his motion. Set the position, velocity, or acceleration and let the simulation move the man for you. |
| Constant Acceleration in One-Dimension | 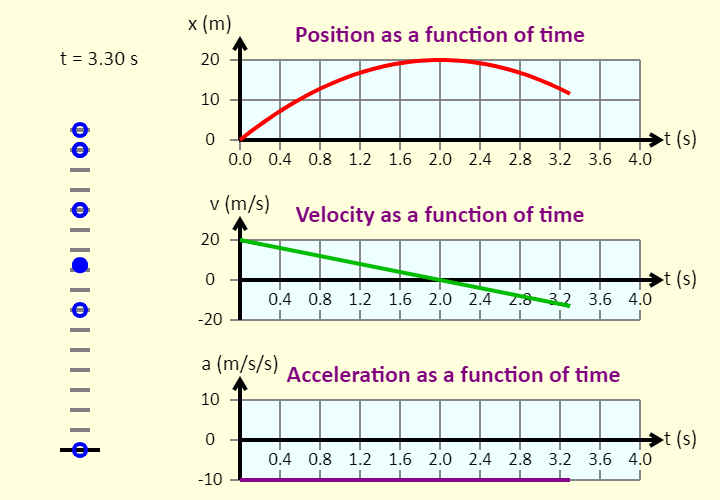 |
This is a simulation of the motion of a ball that is influenced by gravity alone. The ball is either released from rest from a height of 20 meters above the ground, or it is launched straight up from the ground with an initial speed of 20 m/s. |
| Landing a Rocket | 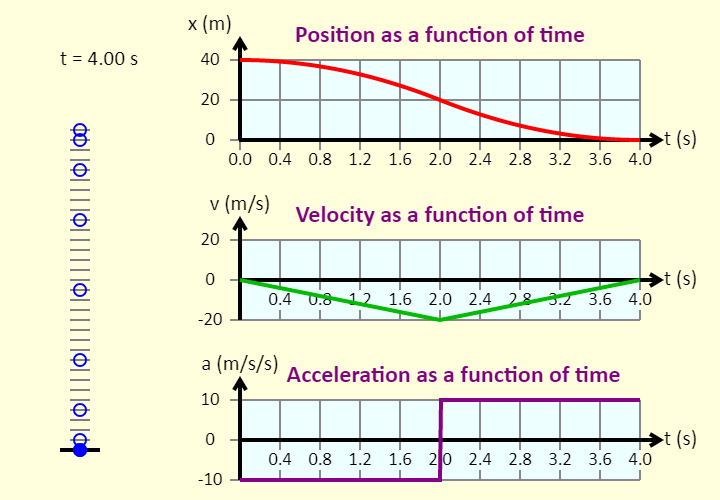 |
Before running the simulation, read the description of the motion below and see if you can predict what the different graphs will look like. Up is positive, and the origin is ground level. This is a simulation of the motion of a ball that has a rocket engine mounted underneath it. The ball is released from rest from a height of 40 meters above the ground, and it falls 20 meters under the influence of gravity alone. At that point, the rocket engine kicks in, giving the ball an upward acceleration of 10 m/s/s (as opposed to the acceleration downward of 10 m/s/s that it just had). You can see the ball's motion diagram, with the position marked at 0.5 s intervals, as well as graphs of the ball's position, velocity, and acceleration, all as a function of time. |
| Ball Sliding Down a Ramp | 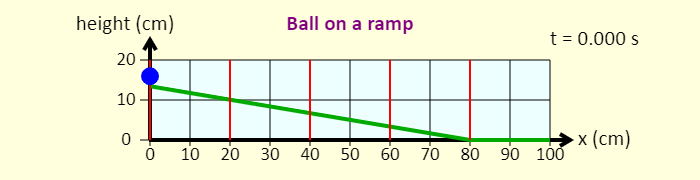 |
The simulation beeps each time the ball passes one of the vertical red lines. Just like the bells on Galileo's ramp, the positions of three of the vertical red lines can be adjusted. The first line and the last line are fixed in place, but the sliders allow you to adjust the positions of the second, third, and fourth lines. Move the lines around until the beeps occur at regular time intervals (make sure the sound is on, on your computer or mobile device). |
| Block on Inclined Plane |
Simulation of a block sliding down an inclined plane (with or without friction). The user can change various parameters and watch the motion of the block as it slides down the plane. |
|
| Relative Velocity in One-Dimension |
This simulation involves relative velocity in one dimension. It is an out-and-back race between two women. Mia runs on the moving sidewalk, while Brandi runs on the non-moving floor. Under what conditions is the race a tie? Under what conditions does Mia win? Under what conditions does Brandi win? |