Magnetic Forces and Magnetic Fields

Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations


Student Learning Objectives



Lessons / Lecture Notes

PY106 Notes from Boston University (algebra-based):

Physics 2B notes from Dr. Bobby W.S. Lau (algebra-based)

HyperPhysics (calculus-based)

Physics 4B notes from Dr. Bobby W.S. Lau (calculus-based)



Important Equations (for algebra-based Physics)
word
pdf



Example Problems

Example Problems for algebra-based physics (from College Physics 2nd Edition by Knight, Jones, and Field):

Example Problems (Magnetic Fields and Forces)
Solutions to Example Problems (Magnetic Fields and Forces)

Example Problems for calculus-based physics (from Fundamentals of Physics 9th Edition by Halliday, Resnick, and Walker):

Example Problems (Magnetic Fields) | Example Problems (Magnetic Fields Due to Currents)
Solutions to Example Problems (Magnetic Fields) | Solutions to Example Problems (Magnetic Fields Due to Currents)



Applets and Animations
Magnetic Field of a Bar Magnet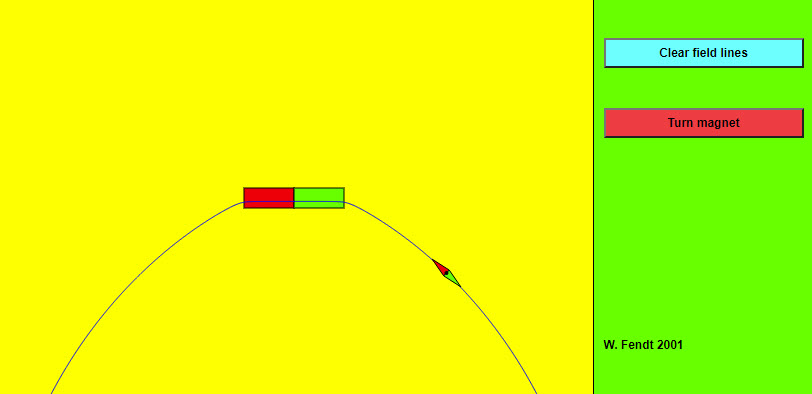

The magnetic field of a bar magnet can be investigated with a compass needle. The magnetic poles of both bar magnet and compass needle are symbolized by the following colours:

north pole red
south pole green

If you move the magnetic needle with pressed mouse button, the magnetic field line through the center of the compass needle will be drawn with blue colour. The blue arrows mark the direction of the magnetic field which is defined as the direction indicated by the north pole of the compass needle. If you turn the magnet by using the red button, the direction of the field lines will reverse. The other button makes it possible to clear all field lines.
Magnet and Compass

Ever wonder how a compass worked to point you to the Arctic? Explore the interactions between a compass and bar magnet, and then add the earth and find the surprising answer! Vary the magnet's strength, and see how things change both inside and outside. Use the field meter to measure how the magnetic field changes.
Magnetic Fields
Simple animation showing the magnetic field surrounding a bar magnet.
Ferromagnetism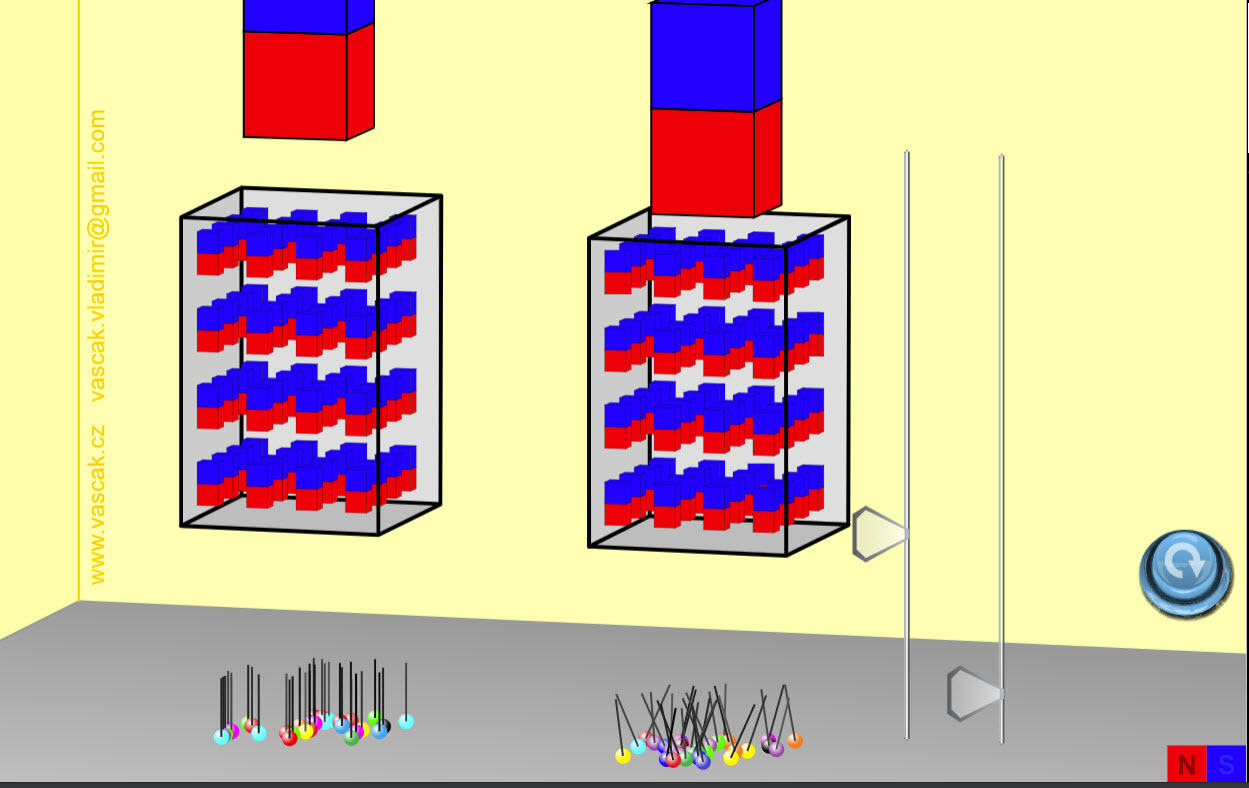

Simple animation showing ferromagnetism.
Magnets and Electromagnets
Explore the interactions between a compass and bar magnet. Discover how you can use a battery and wire to make a magnet! Can you make it a stronger magnet? Can you make the magnetic field reverse?
Lorentz Force

This HTML 5 app demonstrates the Lorentz force, exerted on a current-carrying conductor swing in the magnetic field of a horseshoe magnet.

You can switch on (off) the current by using the upper button ("On / Off"). The other two buttons ("Reverse current" and "Turn magnet") make it possible to change the direction of the current respectively of the magnetic field. If the corresponding checkboxes are selected, the app will indicate the conventional direction of current (red arrows), the magnetic field lines (blue) and the Lorentz force (black arrow).
Magnetic Field of a Straight Current-Carrying Wire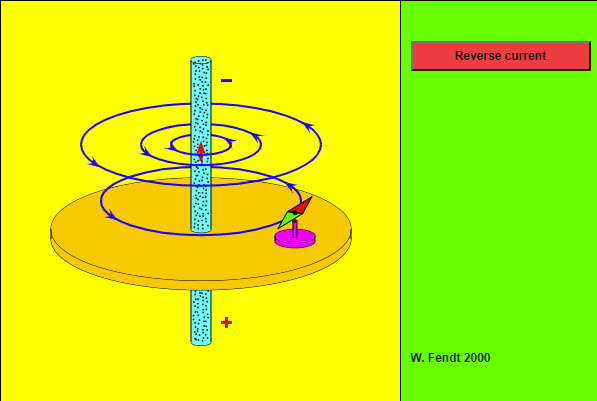

An electric current produces a magnetic field. This applet simulates an experiment concerning the magnetic field of a straight current-carrying wire. A large current passes through a vertical wire. You can reverse the direction of this current by using the red button. The signs at the ends of the wire symbolize the poles of the connected battery. The conventional direction of current is given by the red arrow. Note that the motion of the electrons (green dots) is opposite to the conventional direction!

A compass needle which can be moved (by dragging the mouse with pressed mouse button) shows the direction of the magnetic field (blue) at a given position. North and south pole of the compass needle are painted with red respectively green colour. The influence of the earth's magnetic field is neglected in this simulation.
Ampere's Right Hand Screw Rule 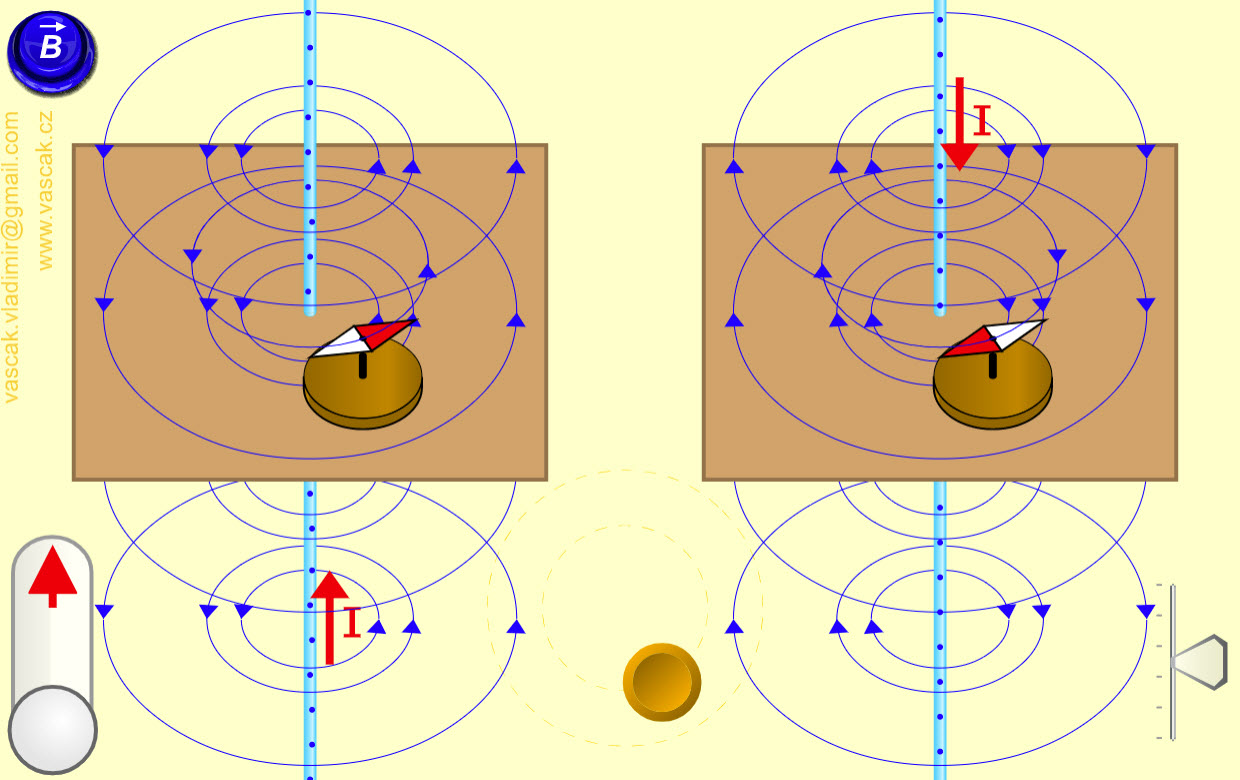Nice applet showing how to use the right-hand rule to determine the magnetic field around a current-carrying wire.
Magnetic Field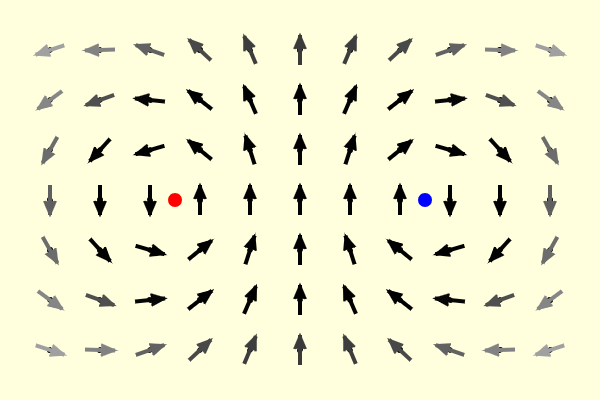

The simulation shows the magnetic field near two long-straight current-carrying wires.
If the wire is drawn in red, the current is directed out of the screen.
If the wire is drawn in blue, the current is directed into the screen.

You should be able to click-and-drag the wires to move them around the screen, and use the sliders to change the currents.
Magnetic Field in 1-D 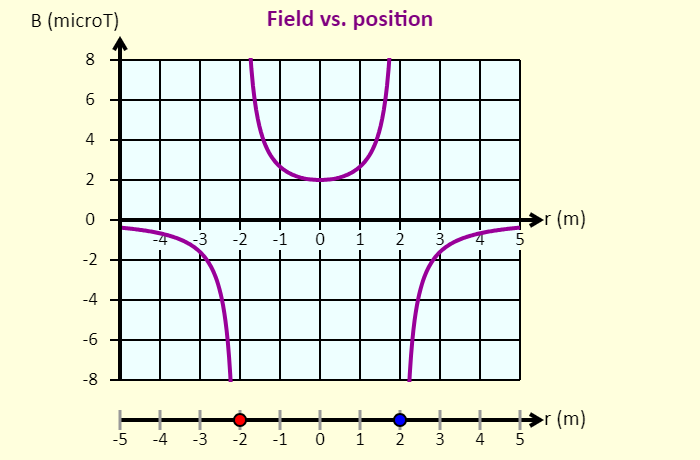Click-and-drag the wires to move them left or right. The wire on the left is confined to the region to the left of the origin; the wire on the right is confined to the region to the right of the origin. In this simulation, you can see the graph of the magnetic field on the x-axis as a function of position. On the graph, the magnetic field is shown as positive if the net field at that position is directed up, and the field is shown as negative if the field is directed down. Using the sliders, you can adjust the values of the currents.
3-D Magnetostatic Field Simulation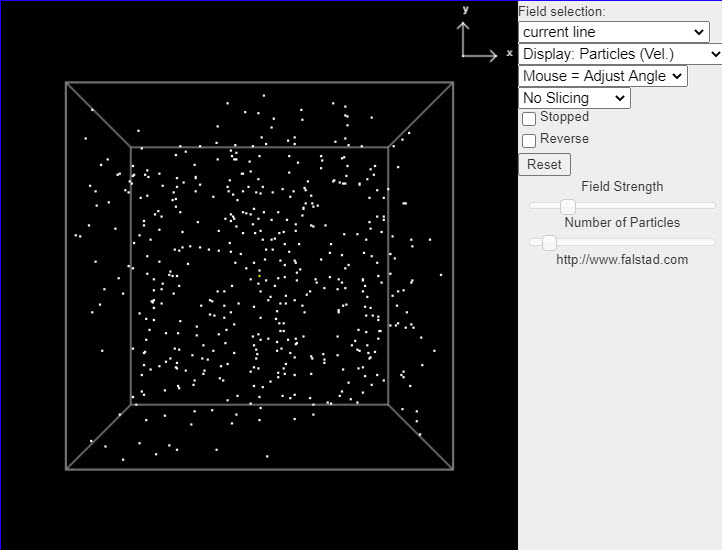

This java applet is a magnetostatics demonstration which displays the magnetic field in a number of situations. You can select from a number of fields and see how particles move in the field if it is treated as either a velocity field (where the particles move along the field lines) or an actual force field (where the particles move as if they were little magnets). This helps you visualize the field. You can also view the vector potential (A).

The menu in the upper right has a variety of different fields to choose from.
Charge in a Magnetic Field 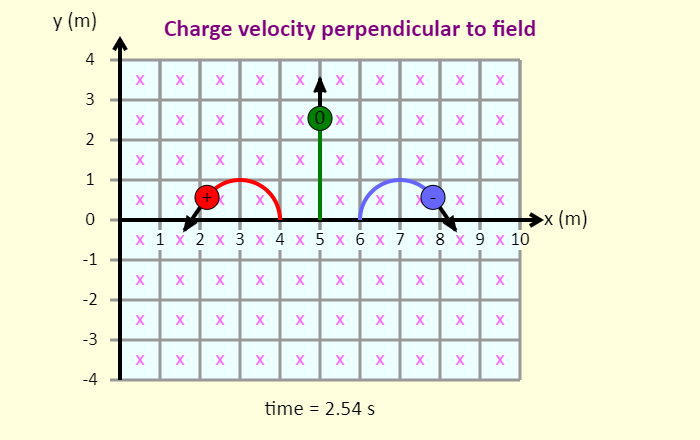In this simulation, you can investigate the force that a magnetic field exerts on a charged particle. This force has some things in common with the force an electric field exerts on a charged particle, but there are also key differences between them. One thing that is apparent in the simulation is that one possible outcome of a magnetic field applying a force on a charged particle is that the particle experiences uniform circular motion, so exploring the magnetic force will also give you a chance to review circular motion concepts.
Charge in a Magnetic Field 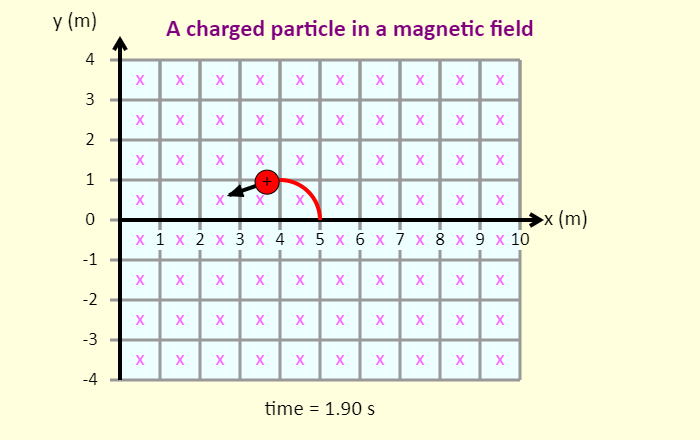In this simulation, you can play with the direction of the magnetic field and the magnitude and sign of the charge to draw patterns on the screen. Explore the different patterns you can make. See how long you can run the simulation without the trail crossing and without the charge going outside the grid. Note that the field is either into the screen (marked with x's) or out of the screen (o's).
Moving Charge in a Magnetic Field 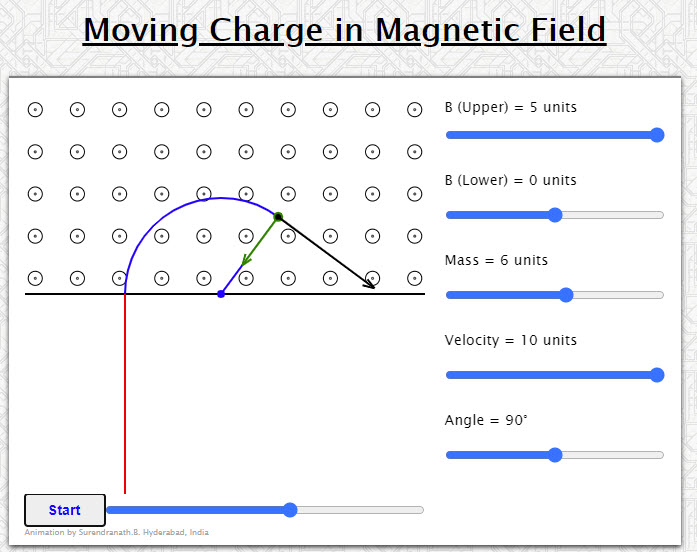Animation shows a charged particle moving in two magnetic fields. It can be made to cross the boundary between the two fields using appropriate values for magnetic field in the lower region and the velocity of the charged particle.
Veocity vector is shown in black color and the force vector is shown in green color.
Drag to see different parts of the path.
Moving Charge in Electric & Magnetic Fields 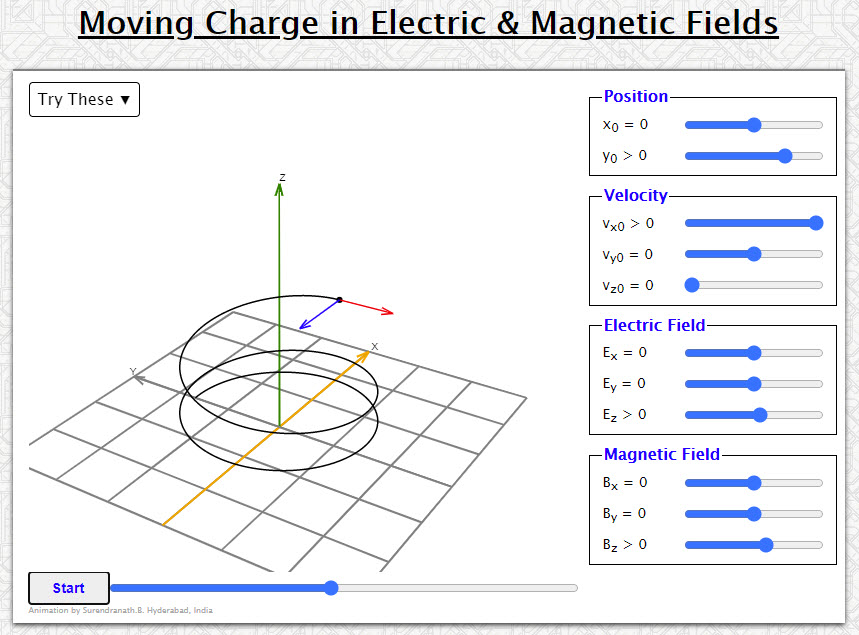Animation shows the motion of a positive charged particle subject to Lorentz force.
Magnetic field on the axis of a circular coil 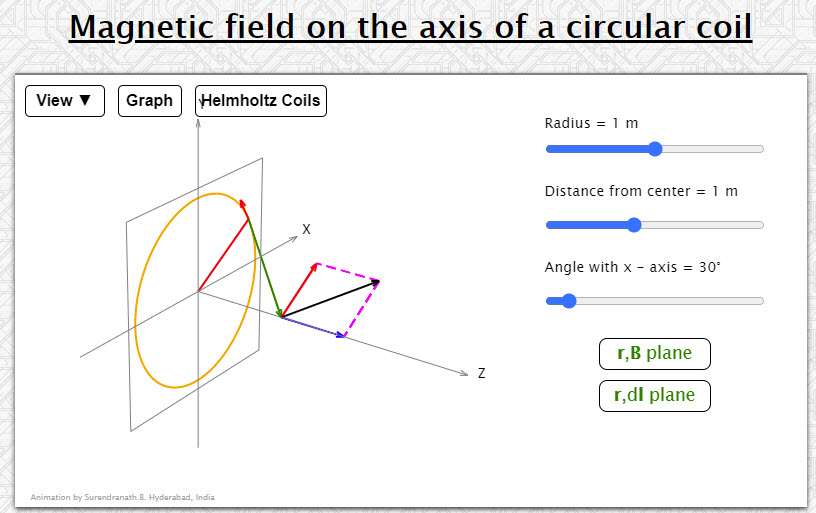Animation shows the magnetic induction vector due to a differential element of a circular wire on the axis of the circle. The red vector is the dl element, the green vector the radius vector r of the point on the axis relative to the element and the black vector dB is the magnetic induction vector due to the element. The components parallel and perpendicular to the axis are shown in blue and red colors.Dragging in vertical/horizontal directions changes orientation of the coil.
Charge in a 3-D Magnetic Field 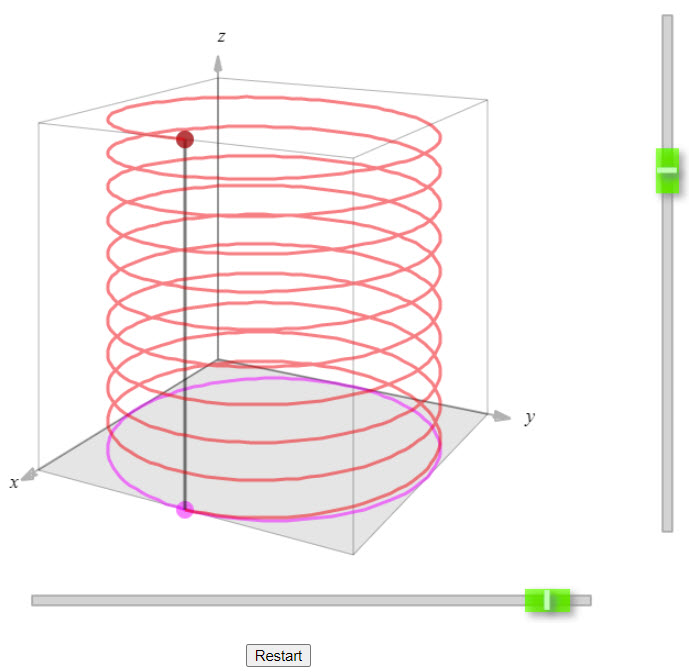This simulation shows the spiral path followed by a positively charged particle (in red) in a uniform magnetic field. Also shown are the two components of the motion. The purple path shows the circular motion of the particle, coming from the velocity component that is perpendicular to the magnetic field. The black path shows the constant-velocity motion associated with the velocity component that is parallel to the field. The combination of the circular motion and the straight-line motion produces a spiral. Knowing that the particle is positive, you should be able to determine the direction of the magnetic field.
Mass Spectrometer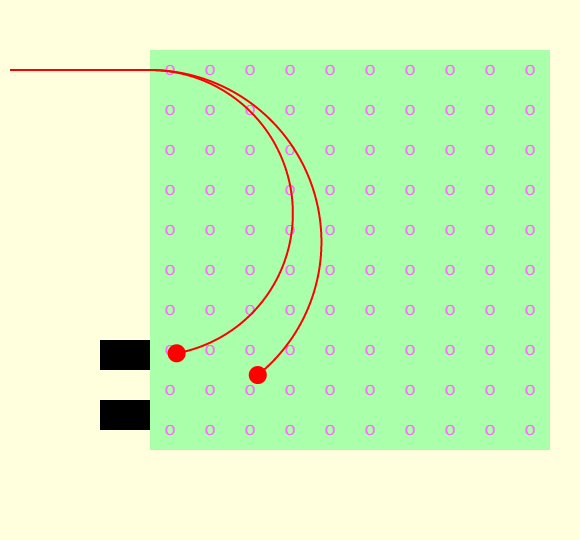

This simulation shows the three phases in a mass spectrometer.

In the acceleration phase, a particle with a positive charge is released from rest near the positive plate of a parallel-plate capacitor. The particle accelerates across the gap and comes out a hole in the negative plate. Adjust the electric field to see how that affects the particle.

In the velocity selector, there is both a downward directed electric field and a magnetic field directed into the page. The electric field applies a downward force to the particle, and the magnetic field applies a force that is initially upward. Adjust the speed of the particle and observe how the path the particle follows is affected.

Only particles that pass undeflected through the velocity selector enter the mass separator, which is simply a region with a uniform magnetic field directed out of the page. The radius of the path followed by a particle is proportional to the mass of the particle, so particles are separated by mass.
Cyclotron 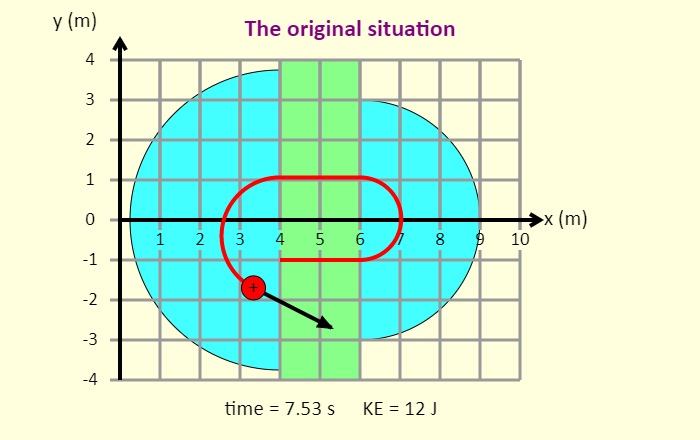This is a simulation of a cyclotron, which is a very compact particle accelerator. In the D-shaped sections (these are called dees) there is a uniform magnetic field that makes the positively charged particle follow a path that is a half circle. Each of these half circles brings the particle back to the gap between the dees, in which there is an electric field that accelerates the particle across the gap. Eventually, the particle comes flying out of the cyclotron at high speed.