Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations
Student Learning Objectives
Lessons / Lecture Notes
PY105 Notes from Boston University (algebra-based):
Physics 2A notes from Dr. Bobby W.S. Lau (algebra-based)
HyperPhysics (calculus-based)
Important Equations (for algebra-based Physics)
|
|
|
|
word
|
pdf
|
Example Problems
Example Problems for calculus-based physics (from Physics for Scientists and Engineers 4th Edition by Knight):
Example Problems (Rotation of a Rigid Body)
Solutions to Example Problems (Rotation of a Rigid Body)
| Center of Mass | 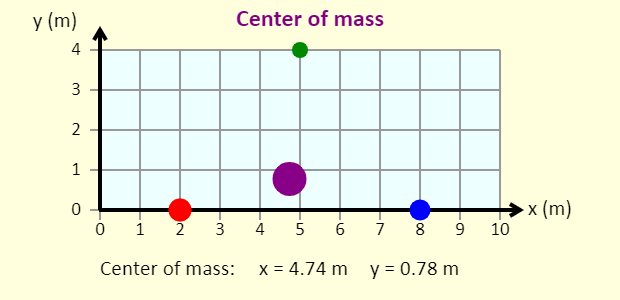 |
This simple animation shows the location of the COM for a three particle system. |
| Motion of Center of Mass | 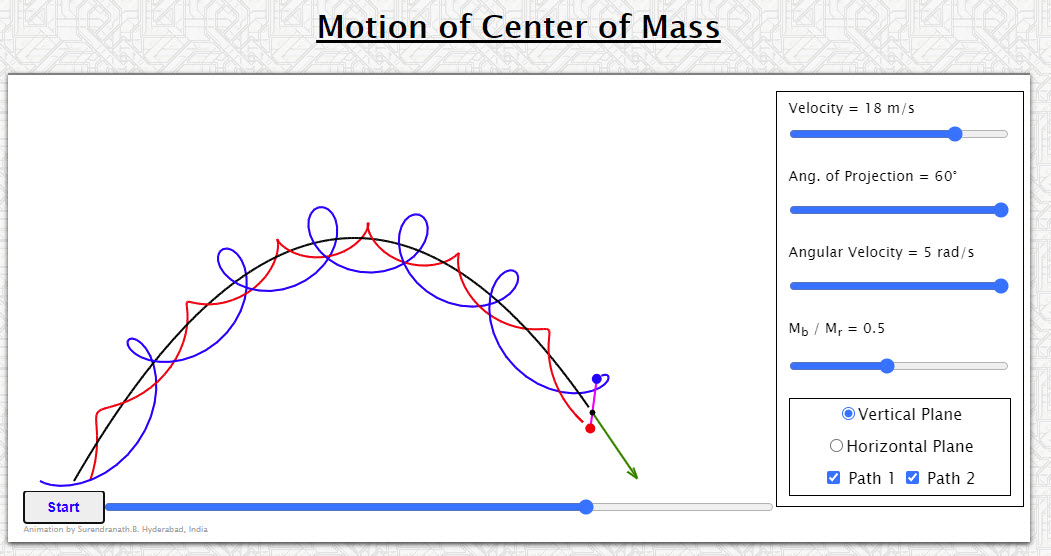 |
Animation shows the motion of center of mass of a two particle system. Should help to bring to focus the importance of the center of mass in analyzing the behavior of system of particles. |
| Motion of Center of Mass |
This simulation illustrates the power of the concept of the center of mass - different points on an object follow complicated paths as the object flies through the air, but the object's center of mass follows a simple parabolic trajectory, the same path a ball would follow. |
|
| Rotational Kinematics and Constant Acceleration in 1D | 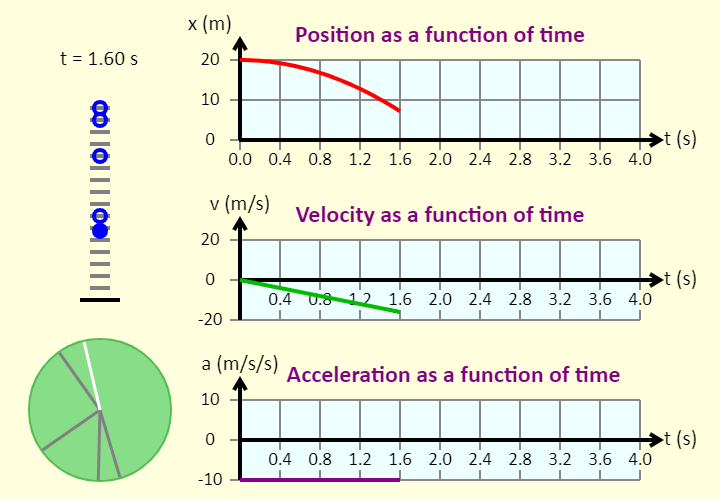 |
In this simulation, you can compare the motion of a ball, which is influenced by gravity alone, to that of a disk, which has a constant angular acceleration directed counter-clockwise. You can see the ball's motion diagram, with the position marked at 0.5 s intervals. You can also see the disk's motion diagram, with the position marked at 0.5 s intervals. You can then either see graphs of the ball's position, velocity, and acceleration, all as a function of time, or graphs of the disk's angular position, angular velocity, and angular acceleration, all as a function of time. |
| Ladybug Revolution | 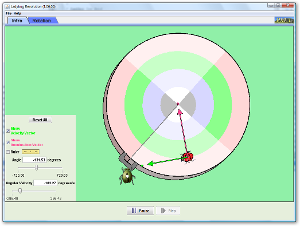 |
Join the ladybug in an exploration of rotational motion. Rotate the merry-go-round to change its angle, or choose a constant angular velocity or angular acceleration. Explore how circular motion relates to the bug's x,y position, velocity, and acceleration using vectors or graphs. |
| Four Views of Rolling | 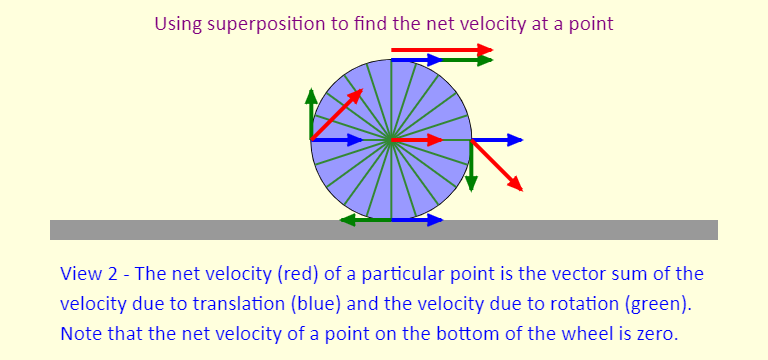 |
The simulation focuses on rolling without slipping, which is the way your tires usually roll when you drive a bike or a car. The simulation shows four different views of rolling - a key to the first three views is that we can look at rolling without slipping as a combination of pure translation (just moving right) and pure rotation, in a way similar to how we looked at projectile motion, as a combination of the horizontal and vertical motions. |
| Rolling and Slipping | 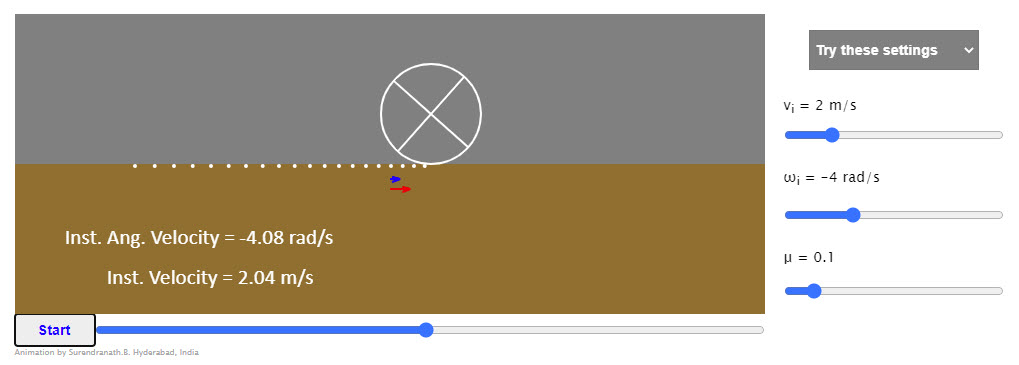 |
The rolling object shown is assumed to have a unit radius. So when linear velocity is numerically equal to angular velocity it rolls without slipping. Further the mass distribution though symmetric about the axis should be assumed to be non uniform. That is, the moment of inertia of the object is not of the standard form. You can set different initial linear and angular velocities. You could vary the coefficient of friction. You would find the object attaining the rolling without slipping condition eventually, whatever the initial conditions. How quickly it does that depending on the friction coefficient. (Set it high if you find the object rolling past the right edge before attaining no slip condition) Observe the red dots. They indicate the position of the center marked at equal intervals of time. If the dots are equidistant, the velocity is not changing. |
| Rolling Races | 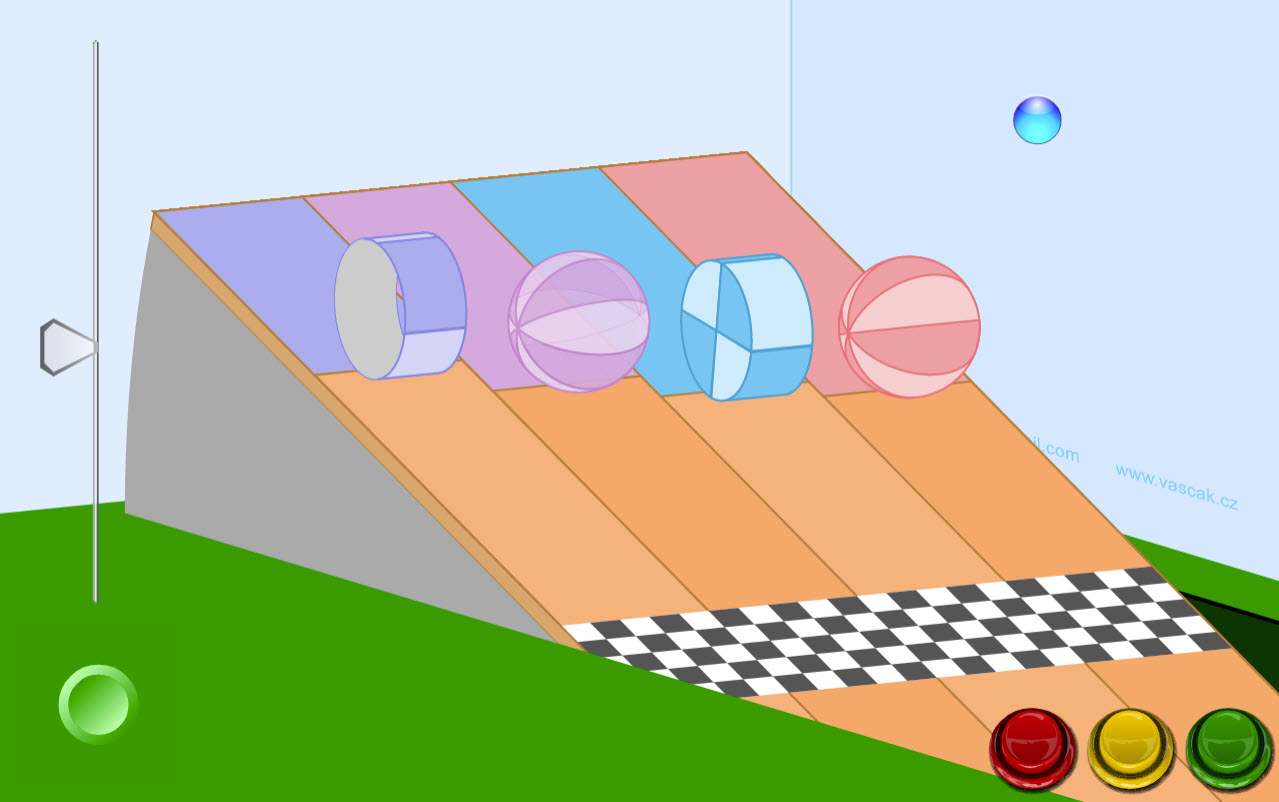 |
Which object will win the rolling race? First make a prediction based upon their moments of inertia and then run the simulation to see if you were correct. |
| Stability on an Incline | 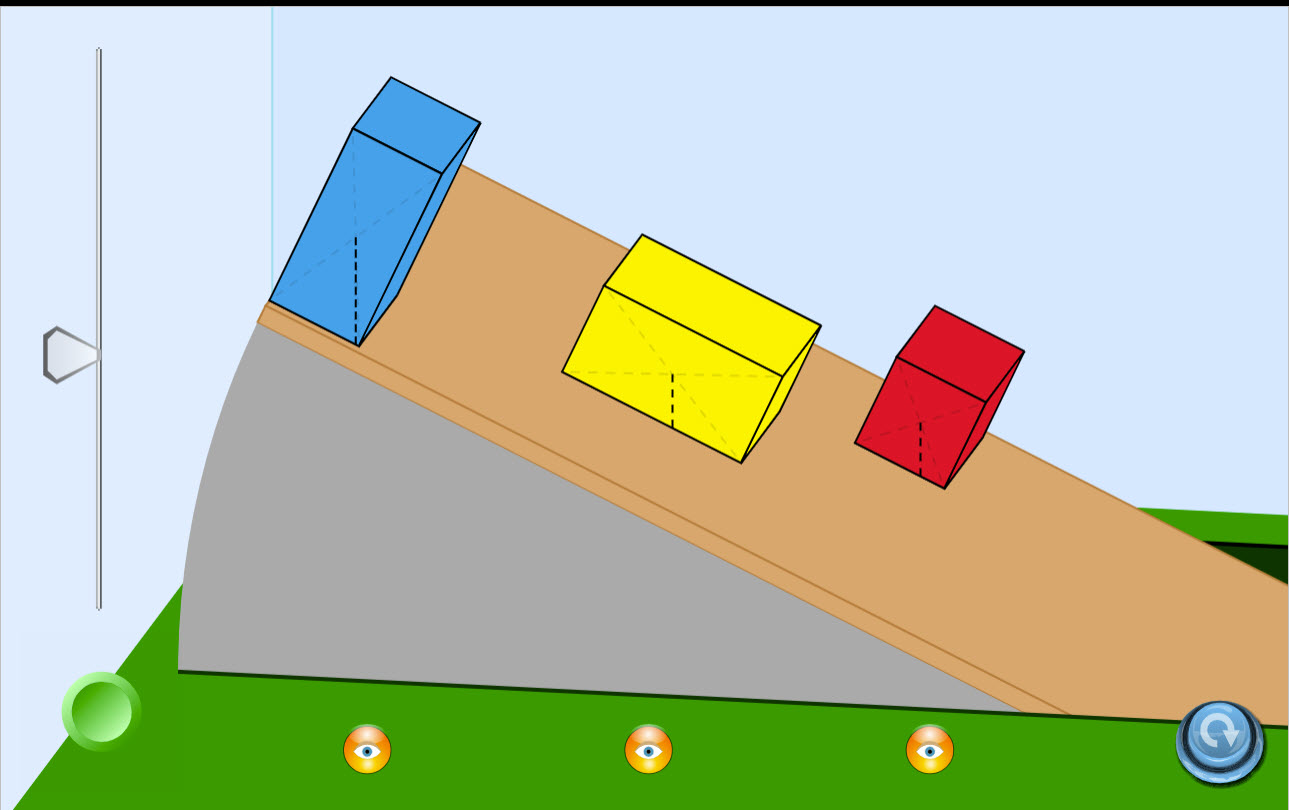 |
Which object will tip over first and why? Run this simulation and find out. |
| Stability |  |
A nice animation showing stability and the role that the support base plays in stability. |
| Torque | 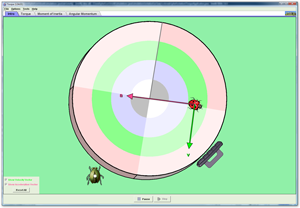 |
Investigate how torque causes an object to rotate. Discover the relationships between angular acceleration, moment of inertia, angular momentum and torque. |
| Three Equivalent Ways to Find Torque | 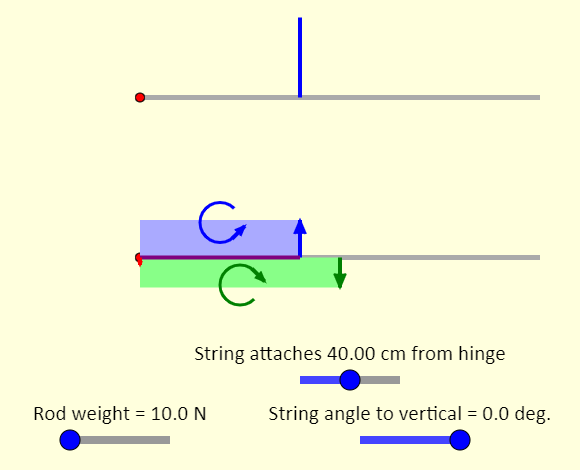 |
This is a simulation of a hinged rod in static equilibrium. The top picture shows the rod, supported by a hinge (in red) at the left end and a blue string at some point along the rod. The second picture of the rod shows the extended free-body diagram of the rod, showing all the forces acting on the rod and where they are applied. The force of gravity is shown in green. The blue force (or force components) represents the tension, and the red force (or force components) represents the hinge force. We'll look at three equivalent ways to find the torque due to the tension. You can use the sliders to control the position and angle of the string, as well as to set the weight of the rod. There is also a checkbox which you can use to show an area representation of torque, the area having units of newton-meters. Taking the axis at the hinge, the torque from the force of gravity acting on the rod is shown in green, and represented by the green rectangle. That torque is directed clockwise. This is offset by the counterclockwise torque from the string. |
| Balance of Moments | 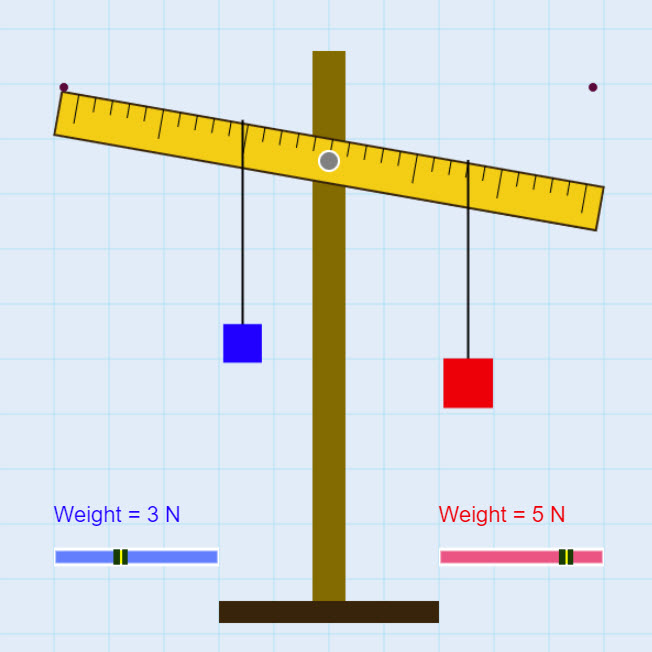 |
Adjust the position of the masses and the weights to see if you can balance the system. |
| Balance the Lever | 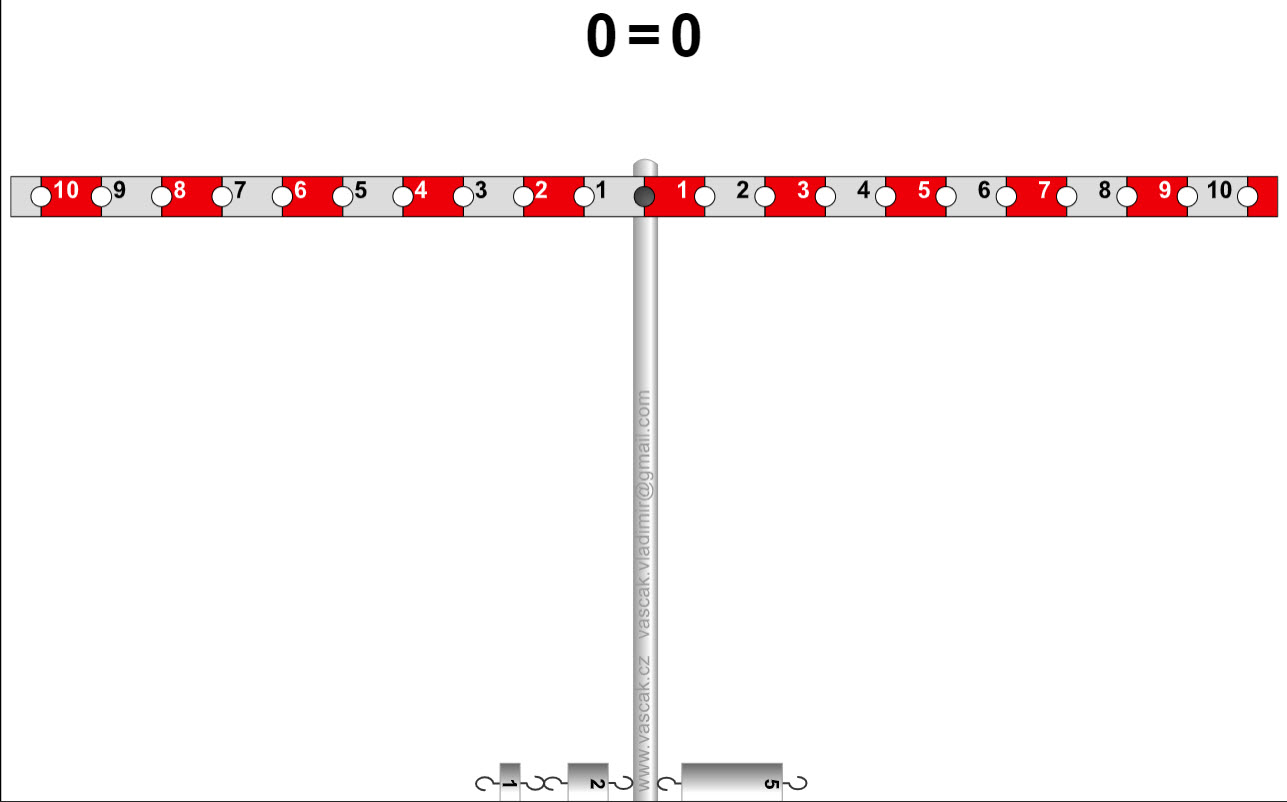 |
A nice applet demonstrating the lever principle and balancing torques. |
| Lever Principle | 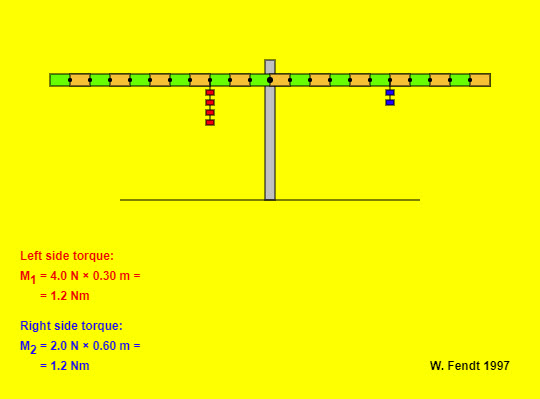 |
This app shows a symmetrical lever with some mass pieces each of which has a weight of 1.0 N. The lever arms can be read from the coloured rectangles; one rectangle corresponds to 0.10 m. The lever is in balance when the app is started. You can attach a new mass piece or put it to another place with pressed mouse button. In a similar way you can remove a mass piece by clicking on it. |
| Balancing Act | 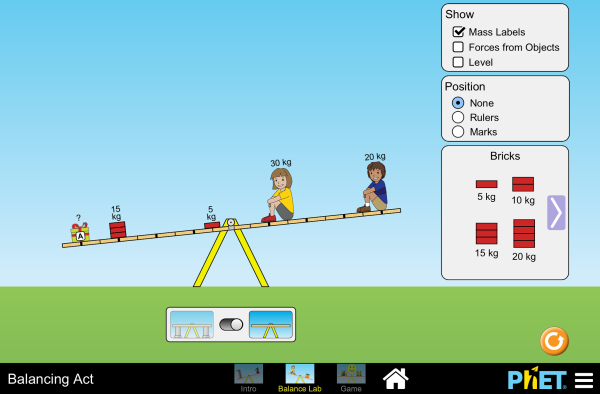 |
Play with objects on a teeter totter to learn about balance. Test what you've learned by trying the Balance Challenge game. |
| How a Front-Wheel-Drive Car Works | 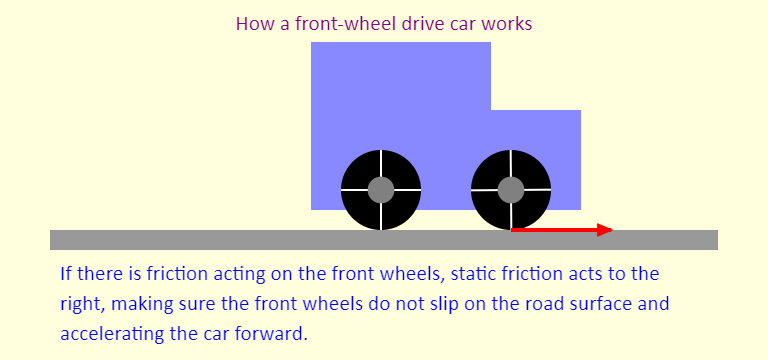 |
This simulation demonstrates the role that friction plays in driving a car. In this case, the car is a front-wheel-drive car. With no friction at all, the engine spins the front wheels but the front wheels just slip on the frictionless road and the car does not move. If there is friction acting on the front wheels only, the force of static friction acts to the right to prevent the front wheels from slipping - this is the force that propels the car forward. Friction on the rear wheels acts left, and is much smaller than friction acting on the front wheels. For the rear wheels, static friction just needs to provide the torque needed to keep the rear wheels rolling without slipping. |
| Atwood's Machine | 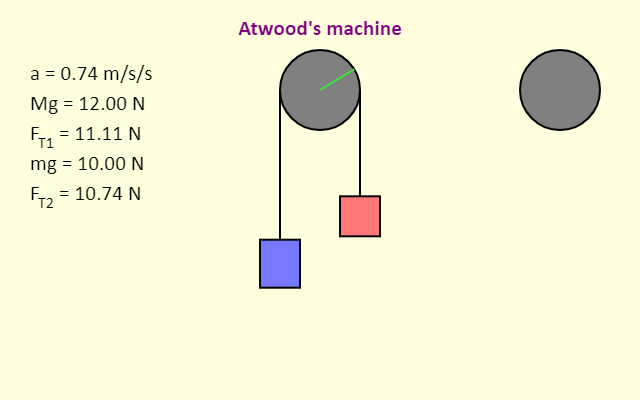 |
The simulation illustrates an Atwood's machine, which is simply two blocks connected by a string passing over a pulley. Unlike the previous version of the simulation, in which the mass of the pulley was negligible, here we account for the mass of the pulley. That leads to the tension in the string being different on the two sides of the pulley, when the system is accelerating. Given the limits on the sliders in the simulation, and the fact that the simulation uses 10.0 m/s/s for g, what are the most positive and most negative values that can be obtained for the acceleration when the pulley mass is 1.0 kg? Note that the pulley has two additional forces that are not shown. These are the downward force of gravity, and the upward normal force (which must balance all the downward forces) - they are omitted because, passing through the center of the pulley, they do not contribute to the torque about the center. |
| Jumping on a Turntable | 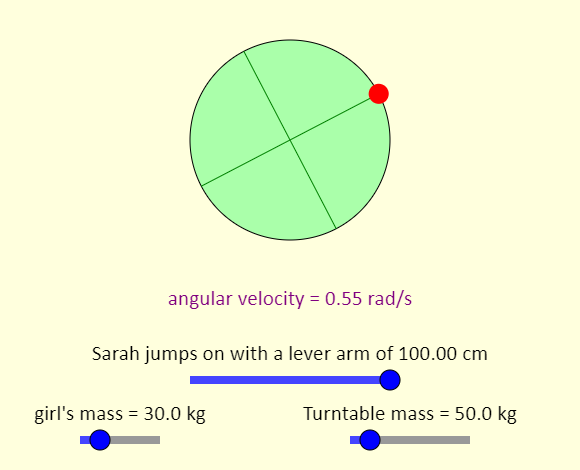 |
This is an overhead view of a red-haired girl called Sarah who jumps onto a playground merry-go-round, or turntable. Using the sliders, you can control the location where the girl jumps on, and the masses of the girl and the turntable. We treat the turntable as a uniform solid disk that rotates without friction about the center. What slider settings will result in the maximum possible value of the angular speed of the system after the collision (after the girl jumps on)? What slider settings will result in the minimum possible angular speed? |
| Spinning Top |  |
Very cool animation allowing you to investigate different aspects and initial conditions of a spinning top. |