Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations
Student Learning Objectives
Lessons / Lecture Notes
The Physics Classroom (conceptual)
PY106 Notes from Boston University (algebra-based):
Physics 2B notes from Dr. Bobby W.S. Lau (algebra-based)
HyperPhysics (calculus-based)
Physics 4B notes from Dr. Bobby W.S. Lau (calculus-based)
Important Equations (for algebra-based Physics)
Example Problems
Example Problems for algebra-based physics (from College Physics 2nd Edition by Knight, Jones, and Field):
Example Problems (Electric Potential)
Solutions to Example Problems (Electric Potential)
Example Problems for calculus-based physics (from Fundamentals of Physics 9th Edition by Halliday, Resnick, and Walker):
Example Problems (Electric Potential) | Example Problems (Capacitance)
Solutions to Example Problems (Electric Potential) | Solutions to Example Problems (Capacitance)
| John Travoltage |  |
Play with John’s foot and arm to explore when he gets a zap! |
| Van De Graff Generator |  |
Very cool applet showing a Van De Graff genertaor and various set-ups that you can implement. |
| Electric Fields in Two DImensions | 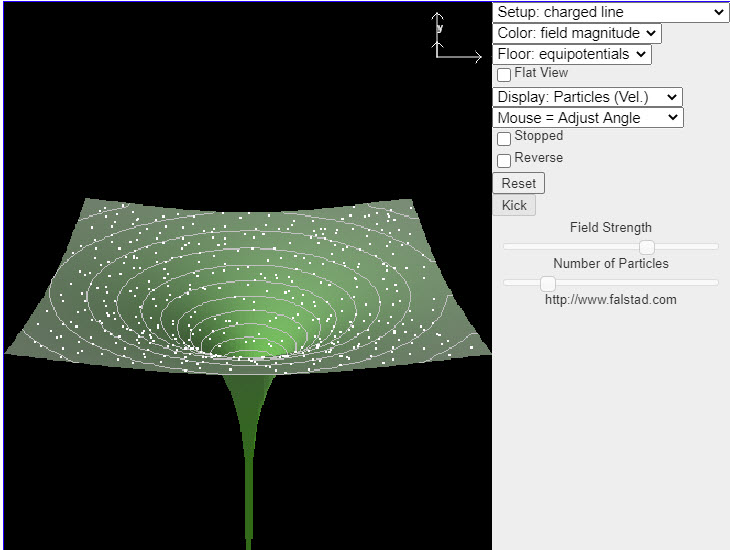 |
This java applet displays the electric field in various situations. You may select one of many fields from the Setup menu in the upper right. The applet shows the potential surface of the field, with particles following the field vectors. You may click and drag with the mouse to rotate the view. Also some of the field selections have parameters which may be adjusted. |
| Electric Fields in Three DImensions | 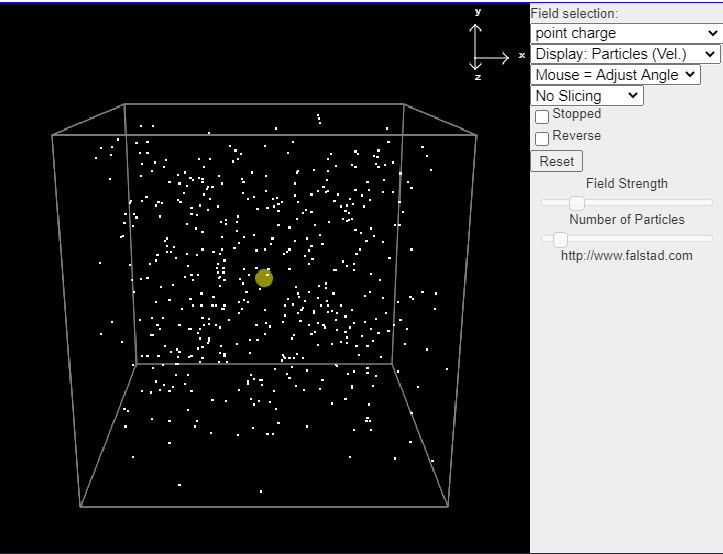 |
This java applet is an electrostatics demonstration which displays the electric field in a number of situations. You can select from a number of fields and see how particles move in the field if it is treated as either a velocity field (where the particles move along the field lines) or an actual force field (where the particles move as if they were charged particles). This helps you visualize the field. The menu in the upper right has a variety of different fields to choose from. |
| Electric Field and Electric Potential | 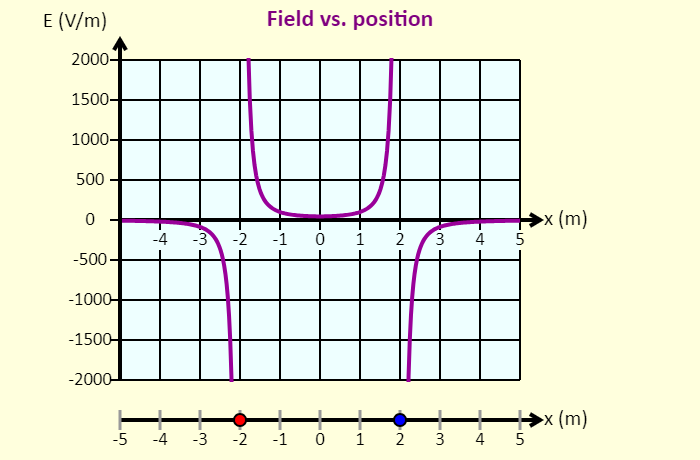 |
Click-and-drag the particles to move them left or right. The particle on the left is confined to the region to the left of the origin; the particle on the right is confined to the region to the right of the origin. In this simulation, you can see the graph of the electric field on the x-axis as a function of position, as well as the electric potential on the x-axis as a function of position. On the graph, the electric field is shown as positive if the net field at that position is directed to the right, and the field is shown as negative if the field is directed left. Using the sliders, you can adjust the charges of the particles. |
| Puzzle - Determine the Charges | 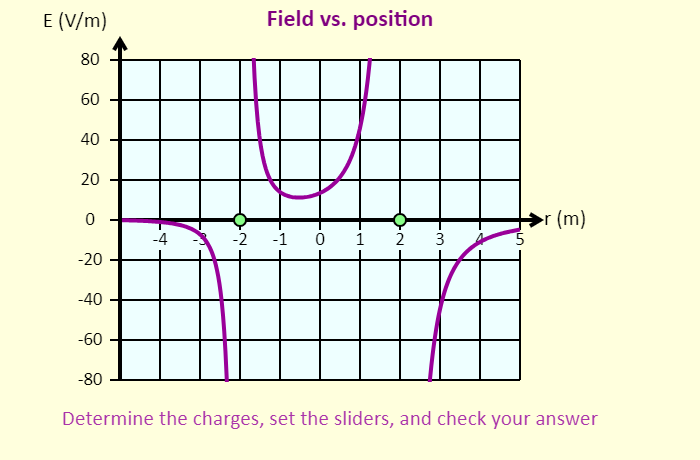 |
In this simulation, the two charged particles (in green) are each randomly assigned a sign and a magnitude that is either 1, 2, 3, 4, or 5 nC. Your goal is to determine their charges, with the help of the graphs - when you have figured out what they are, set the charge sliders to those values and check your answer. You can click-and-drag the particles to move them left or right. The particle on the left is confined to the region to the left of the origin; the particle on the right is confined to the region to the right of the origin. In this simulation, you can see the graph of the electric field on the x-axis as a function of position, as well as the electric potential on the x-axis as a function of position. On the graph, the electric field is shown as positive if the net field at that position is directed to the right, and the field is shown as negative if the field is directed left. Using the sliders, you can adjust the charges of the particles. |
| Potential Energy | 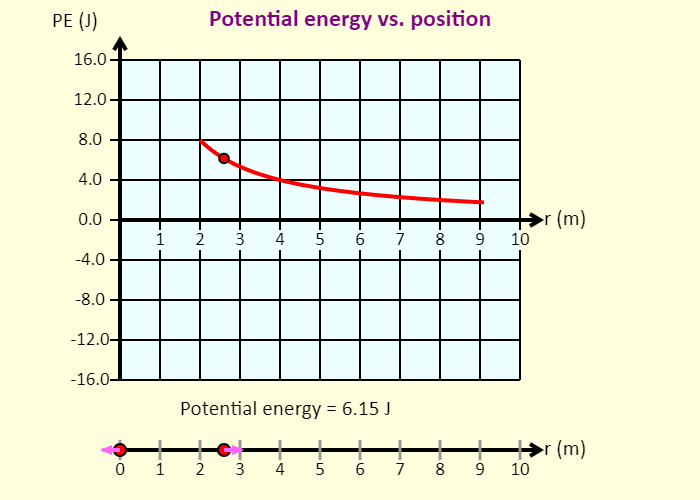 |
Click-and-drag the particles to move them left or right. The particle on the left is confined to the region to the left of the origin; the particle on the right is confined to the region to the right of the origin. In this simulation, you can see the graph of the electric field on the x-axis as a function of position, as well as the electric potential on the x-axis as a function of position. On the graph, the electric field is shown as positive if the net field at that position is directed to the right, and the field is shown as negative if the field is directed left. Using the sliders, you can adjust the charges of the particles. |
| Connections between Force, Field, Potential Energy, and Potential | 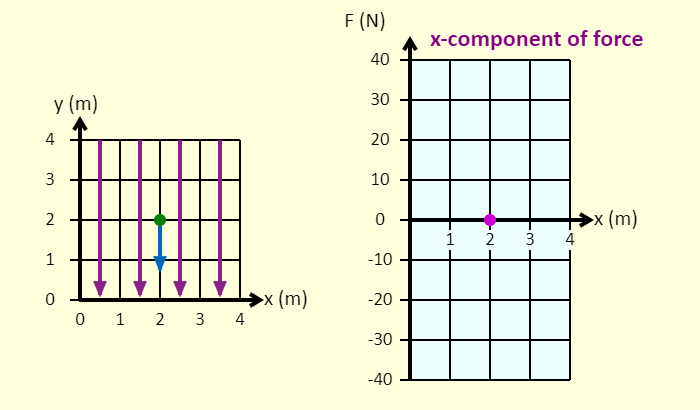 |
On the left is a representation of a 4 m x 4 m space in which there is a uniform field directed down. If you choose a ball, then the field is a gravitational field. If you use a charge, the field is an electric field. On the right is a graph. You can plot six different things on the vertical axis, as a function of either x or y. |
| E,V Graphs | 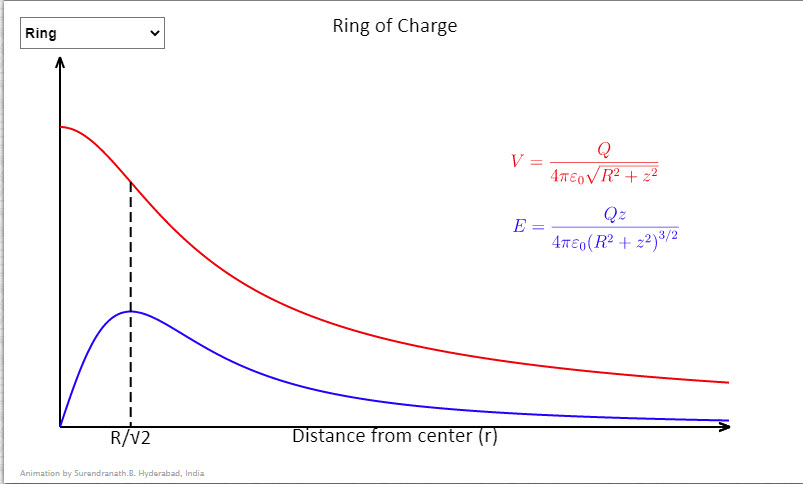 |
Some useful graphs showing variation of potential and field strengths with distance. In the case of the shell charge on the shell is assumed constant and in case of the sphere charge density is assumed constant. In case of concentric shells the charge on the outer shell is double the charge on the inner shell. Radius of the shell/sphere/inner shell can be decreased/increased by taps on left/right halves of the graph. |