Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations
Student Learning Objectives
Lessons / Lecture Notes
The Physics Classroom (conceptual)
PY105 Notes from Boston University (algebra-based):
Physics 2A notes from Dr. Bobby W.S. Lau (algebra-based)
HyperPhysics (calculus-based)
Important Equations (for algebra-based Physics)
Example Problems
Example Problems for algebra-based physics (from College Physics 2nd Edition by Knight, Jones, and Field):
Example Problems (Momentum)
Solutions to Example Problems (Momentum)
Example Problems for calculus-based physics (from Physics for Scientists and Engineers 4th Edition by Knight):
Example Problems (Impulse and Momentum)
Solutions to Example Problems (Impulse and Momentum)
| Momentum and Impulse |
This applet lets you investigate the result of applying a known impulse to a moving object. |
|
| Collisions |
This applet lets you experiment with the collision between two moving carts. You can graph momentum, energy, velocity, and position versus time for different combinations of masses. |
|
| Collisions |
This simulation gives you many perspectives on a one-dimensional collision between two carts. You can see graphs of momentum, kinetic energy, velocity, or position as a function of time. Alternatively, you can see momentum bar graphs showing, for each cart separately as well as the two-cart system, the momentum before the collision, the amount of momentum transferred to the cart or system during the collision, and the momentum after the collision. |
|
| Elastic and Inelastic Collisions | 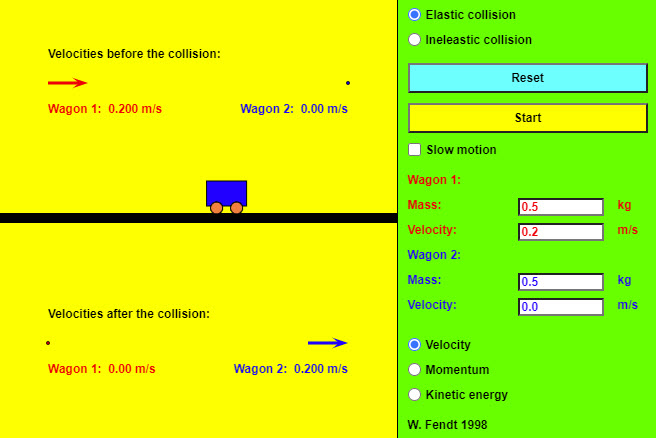 |
This HTML5 app deals with the extreme cases of a collision process illustrated by two wagons: For an elastic collision it is characteristic that the sum of the kinetic energies of the involved bodies is constant. After a perfectly inelastic collision, however, both bodies have the same velocity; the sum of their kinetic energies is reduced, compared with the initial value, because a part of it has changed into internal energy (warming up). The total momentum of the involved bodies is conserved, regardless whether the collision is elastic or inelastic. The movement of the common center of gravity (indicated by a yellow dot) is not influenced by the collision process. You can choose the simulation of an elastic or an inelastic collision by using the appropriate radio button on the top right. The "Reset" button brings the wagons to their initial positions; the animation is started by a mouse click on the "Start" button. If you select the option "Slow motion", the movement will be ten times slower. You can write the values of mass and initial velocity into the textfields. Positive (negative) values of velocity mean a motion to the right (left) side. Extreme inputs are automatically changed. Dependent on the selected radio button (on the bottom right), the app will illustrate the velocities, the momenta or the kinetic energies of the wagons. |
| Collision Lab | 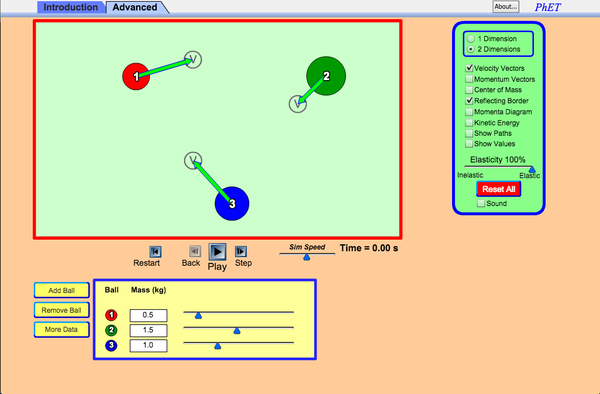 |
Use an air hockey table to investigate simple collisions in 1D and more complex collisions in 2D. Experiment with the number of discs, masses, and initial conditions. Vary the elasticity and see how the total momentum and kinetic energy changes during collisions. |
| 1D Collisions |  |
This applet looks at elastic and perfectly inelastic collisions in one-dimension. |
| 2D Collisions | 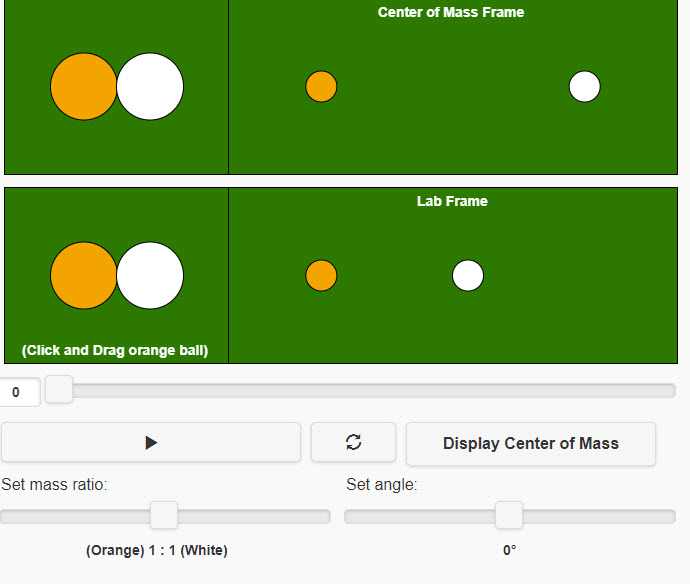 |
This applet looks at two-dimensional collisions. You can look at the collision in the lab frame of the COM frame. |
| Collisions |  |
Animation shows two particles undergoing a collision. The collision can be viewed in the center of mass reference frame or the laboratory frame. The initial velocity in the laboratory reference frame of the striking particle is adjustable. The impact parameter, the mass ratio and the coefficient of restitution can be adjusted using the appropriate sliders. The choice of the reference frame can be made from the drop down list of choices. The slider below the start button can be adjusted to run the animation frame by frame. The vector diagrams show the initial and final momentum vectors of the particles. The green vectors at the moment of contact indicate the direction of the forces acting on the individual particles |
| Newton's Cradle |  |
This nice animation demonstrates Newton's Cradle. The user can adjust the number of balls pulled up on each side. |
| Motion of Center of Mass | 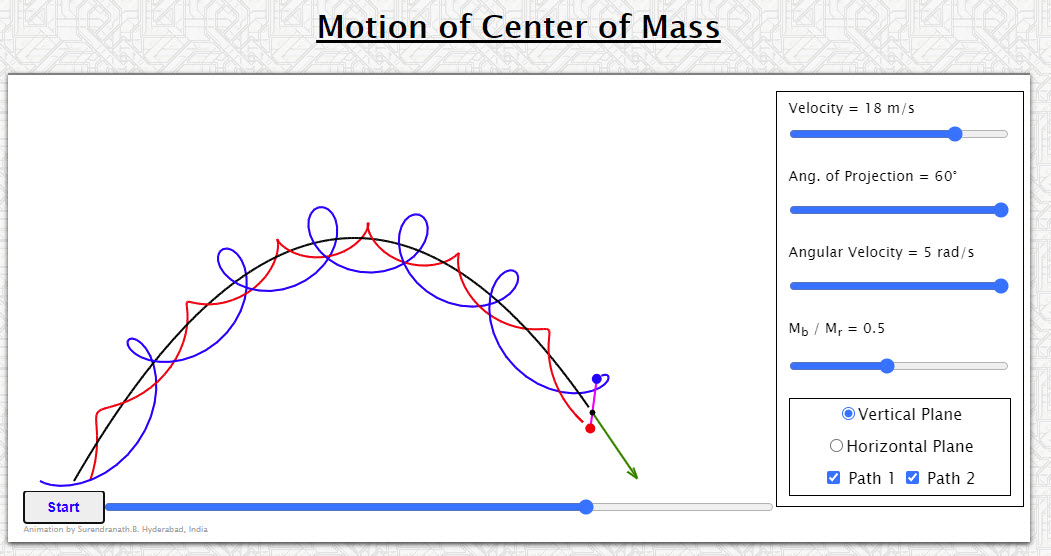 |
Animation shows the motion of center of mass of a two particle system. Should help to bring to focus the importance of the center of mass in analyzing the behavior of system of particles. |
| Center of Mass | 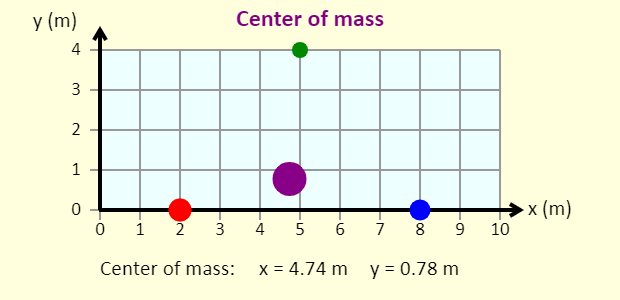 |
This simple animation shows the location of the COM for a three particle system. |
| COM with No External Force | 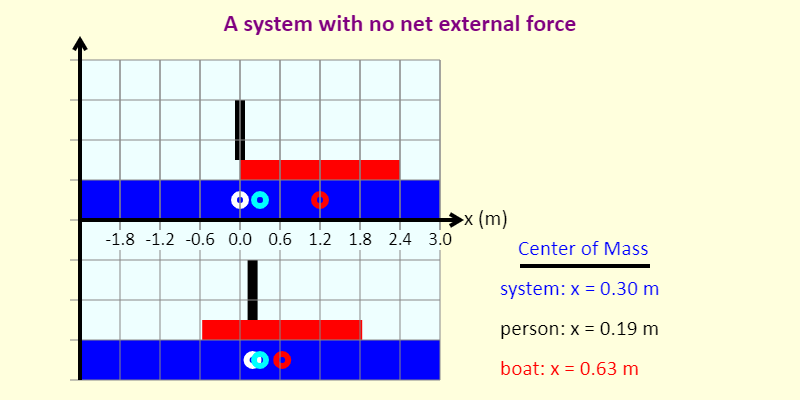 |
The simulation shows a person (in black) standing at the left end of a 2.4-meter-long red boat. The person then moves to the right end of the boat - how far does the boat move? This depends on how the masses of the person and the boat compare. The circles in the water are not life preservers, but instead mark the horizontal positions of the center of mass of the person, the person-boat system, and the boat. |
| Ballistic Pendulum | 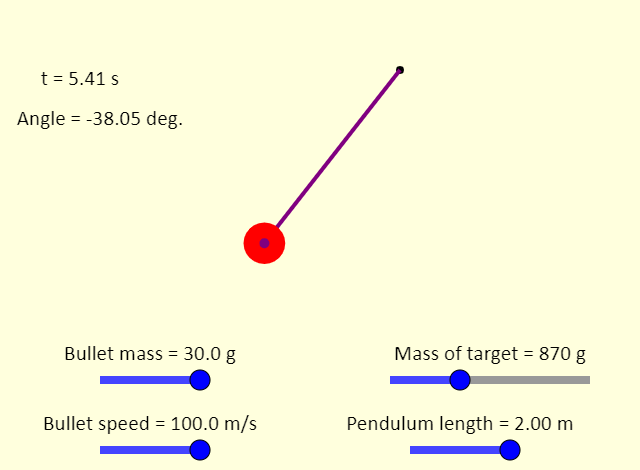 |
A ballistic pendulum is a device that could be used by a crime-scene investigator to determine the muzzle velocity of a gun. The bullet comes out of the gun at high speed, and embeds itself into a target that is hanging from a string. This causes the target (with the bullet embedded) to swing back and forth, pendulum style. By knowing the maximum height that the target reaches, the speed of the bullet can be determined. In this simulation, the speed of the bullet is known (it is set by one of the sliders). Here, determine the maximum height reached by the target in its swing, and then find the increase in the gravitational potential energy of the Earth-target-ball system. Compare this to the kinetic energy of the bullet before the collision. If these two energies are different, explain any differences. Note that the simulation uses g = 9.8 N/kg. |