Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations
Student Learning Objectives
Lessons / Lecture Notes
The Physics Classroom (conceptual)
PY105 Notes from Boston University (algebra-based):
Physics 2A notes from Dr. Bobby W.S. Lau (algebra-based)
HyperPhysics (calculus-based)
Physics 4A notes from Dr. Bobby W.S. Lau (calculus-based)
Important Equations (for algebra-based Physics)
Example Problems
Example Problems for algebra-based physics (from College Physics 2nd Edition by Knight, Jones, and Field):
Example Problems (Vectors & Motion in Two Dimension)
Solutions to Example Problems (Vectors & Motion in Two Dimensions)
Example Problems for calculus-based physics (from Physics for Scientists and Engineers 4th Edition by Knight):
Example Problems (Kinematics in Two Dimensions)
Solutions to Example Problems (Kinematics in Two Dimensions)
| Instantaneous & Average Velocity | 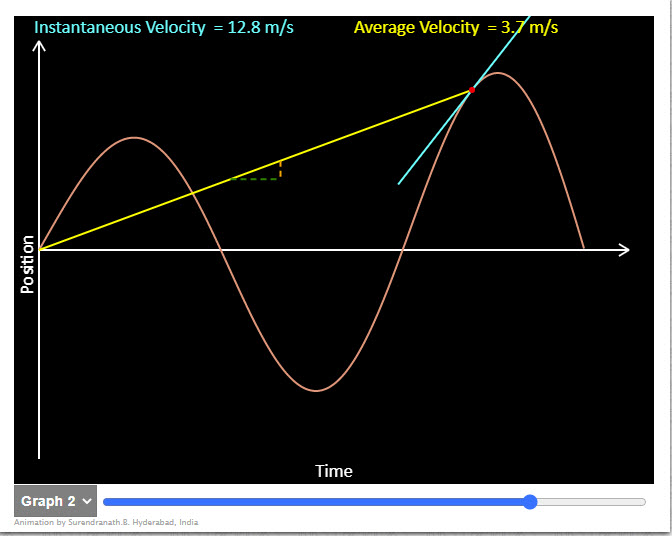 |
Animation shows instantaneous and average velocities in a position time graph. In Graph 1 an object starts accelerating from rest , travels uniformly and then comes to rest. In Graph 2 position time graph of an oscilating object is shown. Graph 3 is for a body projected vertically upwards. Check to see if instantaneous and average velocities become equal at any moment. In Graph 4 an object starts accelerating from rest , and then comes to rest. Average velocity is the slope of the yellow line and Instantaneous velocity is the slope of the cyan line. |
| Ballistics cart | 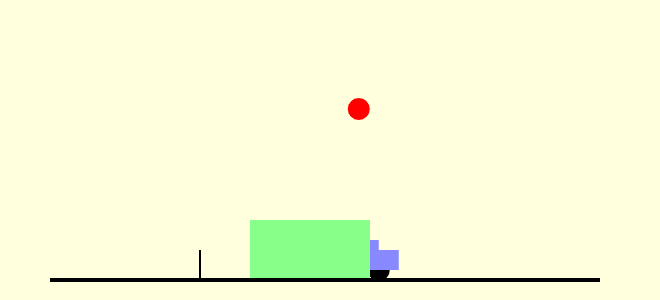 |
The simulation shows a ballistics cart. If the cart is at rest on a horizontal surface, it will shoot a ball straight up in the air, and catch the ball again. What if, as in this simulation, the cart is traveling at a constant velocity horizontally, instead? Will the ball land ahead of the cart, in the cart, or behind the cart? Note that the cart fires the ball straight up, with respect to the cart, when the middle of the cart passes the small vertical trigger on the track. Use the buttons to select the different modes (whether there is a tunnel or not, and whether to show the velocity vectors). |
| Ladybug Motion 2D | 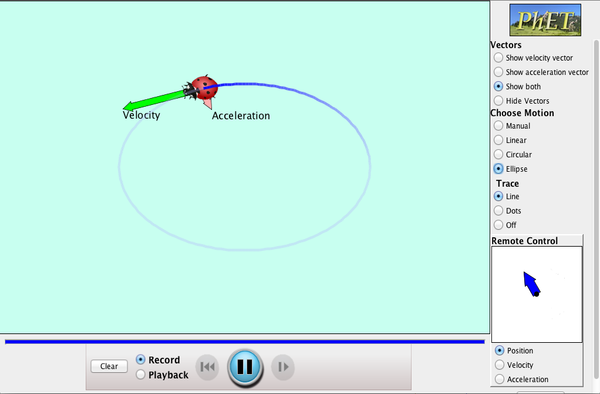 |
Learn about position, velocity and acceleration vectors. Move the ladybug by setting the position, velocity or acceleration, and see how the vectors change. Choose linear, circular or elliptical motion, and record and playback the motion to analyze the behavior. |
| Motion in 2D | 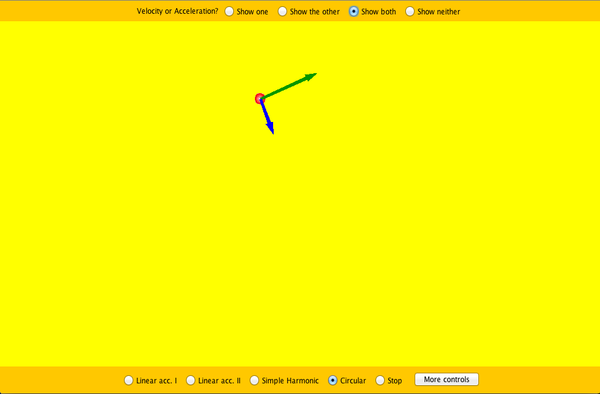 |
Try the new "Ladybug Motion 2D" simulation for the latest updated version. Learn about position, velocity, and acceleration vectors. Move the ball with the mouse or let the simulation move the ball in four types of motion (2 types of linear, simple harmonic, circle). |
| Maze Game |  |
Learn about position, velocity, and acceleration in the "Arena of Pain". Use the green arrow to move the ball. Add more walls to the arena to make the game more difficult. Try to make a goal as fast as you can. |
| Galileo's Compound Representation of Projectile Motion | This simulations shows Galileo's compound representation of projectile motion as a combination of horizontal motion with constant velocity and vertical motion with constant acceleration. | |
| Projectile Motion | 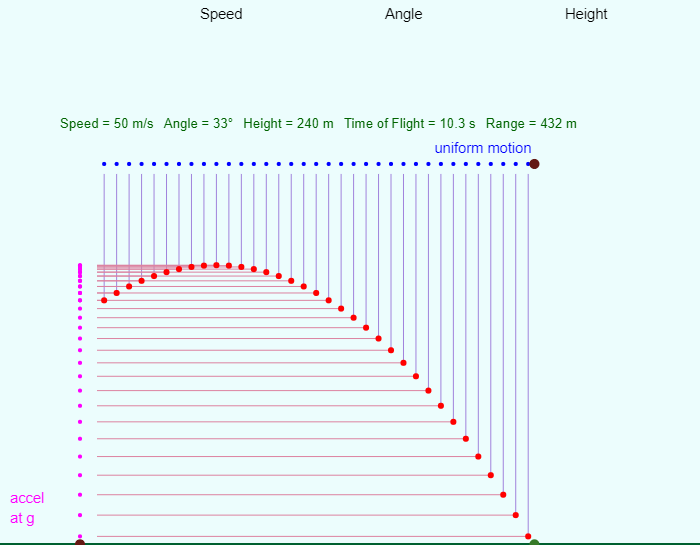 |
An excellent simulation of projectile motion where the user can adjust the initial speed, angle, and height of the projectile. The applet nicely shows the connection between horizontal motion at constant velocity and vetical motion at constant acceleration. |
| Projectile Motion | 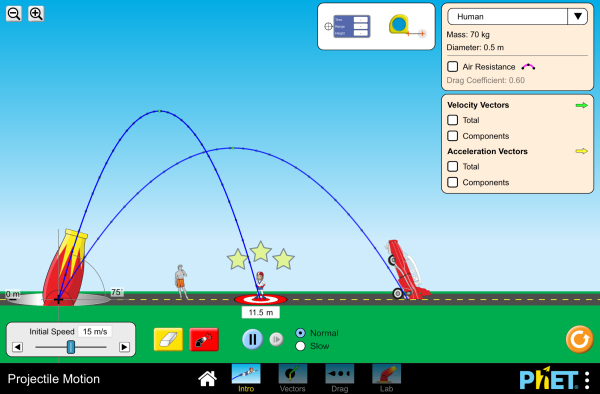 |
Blast a car out of a cannon, and challenge yourself to hit a target! Learn about projectile motion by firing various objects. Set parameters such as angle, initial speed, and mass. Explore vector representations, and add air resistance to investigate the factors that influence drag. |
| Projectile Motion | 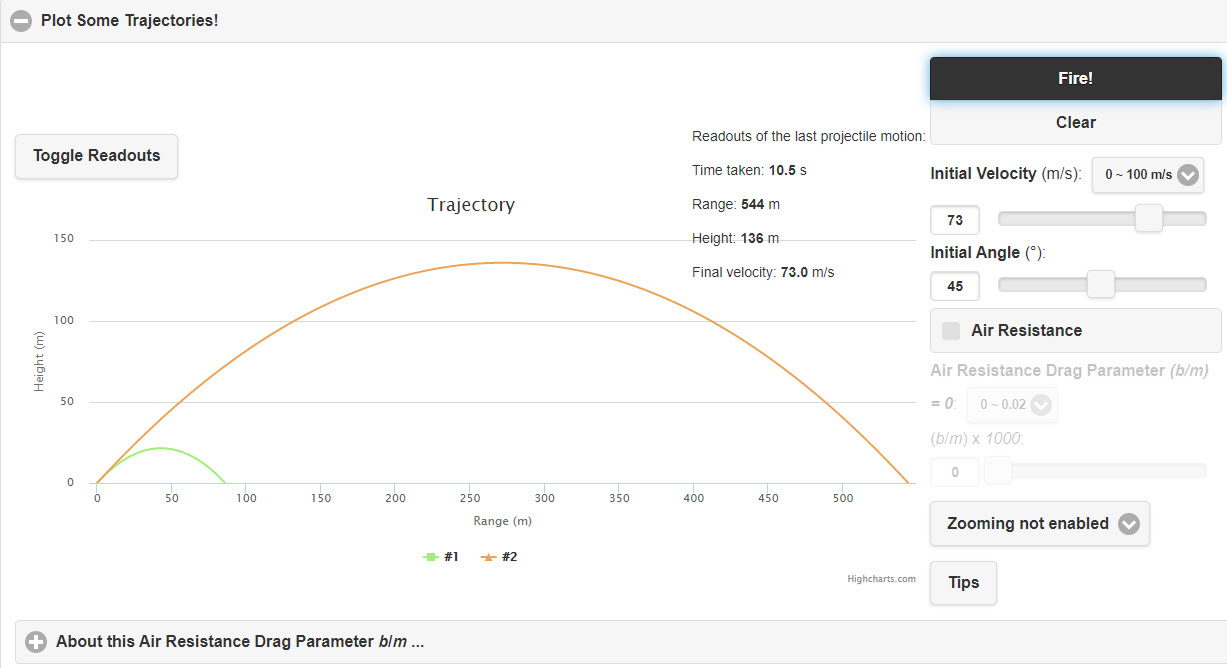 |
Nice applet showing the trajectories of various projectiles with and without air resistance. |
| Velocities & Accelerations | 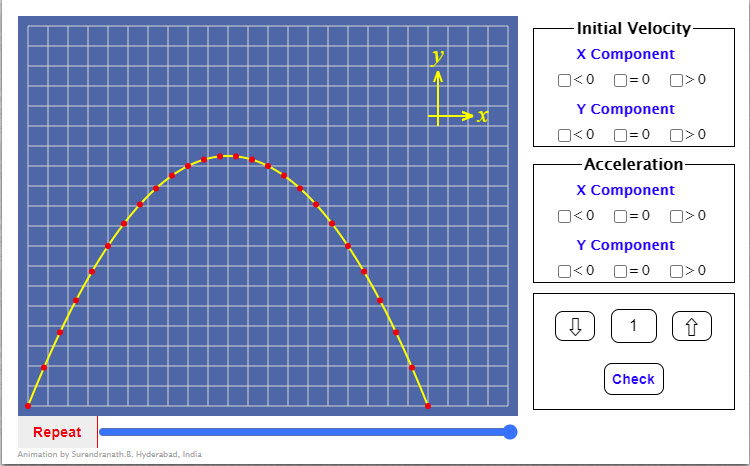 |
Animation is useful in relating to directions of acceleration and velocities in two dimensional motion. Click on start two view an animation. After viewing the animation you should be able to make the right choices in the radio button panel on the right. The check button at the bottom will allow you to verify your answers. You can right/left click on the button with the number to view a different animation. The red dots shown in the animation are postions at equal intervals of time. Do remember the motion shown is hypothetical. Do not assume the physical situation. All conclusions must be based on observation of the motion. |
| Projectile Motion | 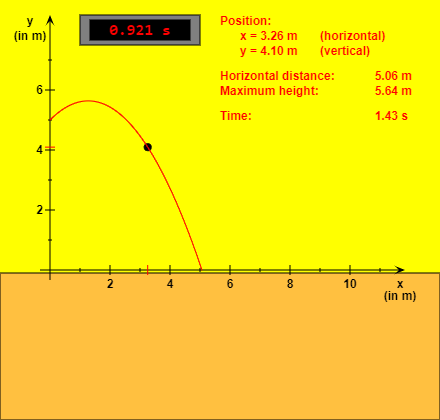 |
This HTML5 app shows the motion of a projectile. The "Reset" button brings the projectile to its initial position. You can start or stop and continue the simulation with the other button. If you choose the option "Slow motion", the movement will be ten times slower. You can vary (within certain limits) the values of initial height, initial speed, angle of inclination, mass and gravitational acceleration. The radio buttons give the possibility to select one of five physical sizes. The effect of air resistance is neglected. |
| A Race | 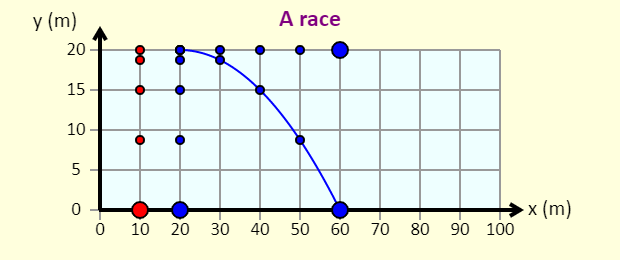 |
This simulation shows a race between a ball dropped from rest and a ball thrown horizontally. |
| Projectile Motion Trajectory | 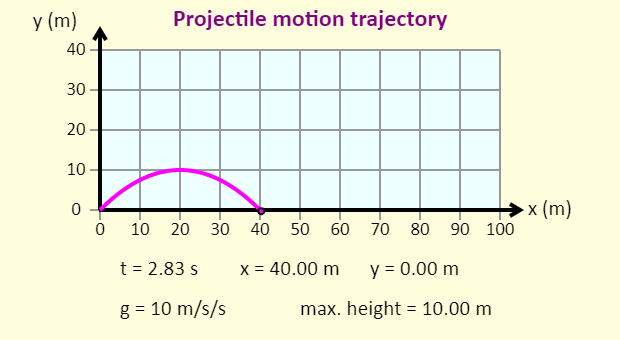 |
Simple applet that shows the trajectory of a projectile fired from the ground without air resistance. |
| Projectile Motion Trajectory | 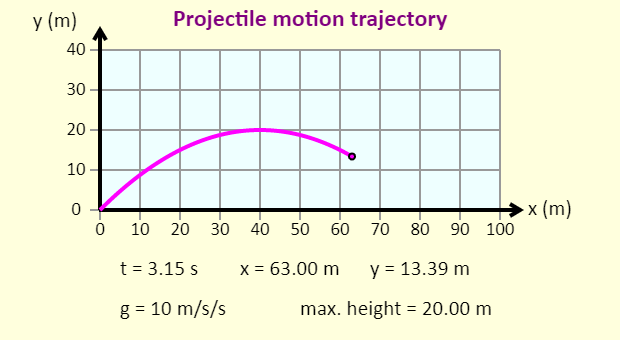 |
Similar to the above applet except that you control the x- and y-components of the initial velocity. |
| Projectile Motion | 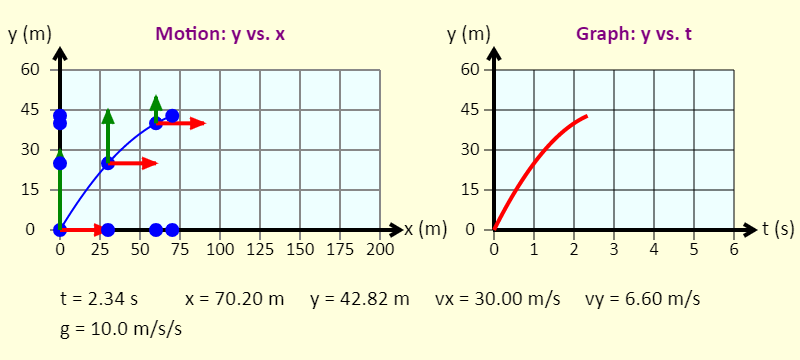 |
The simulation shows a ball experiencing projectile motion, as well as various graphs associated with the motion. Use the buttons to select different values of g (the acceleration due to gravity), the horizontal component of the initial velocity, the vertical component of the initial velocity, and what to plot on the vertical axis of the graph (on the right). A motion diagram is drawn, with images of the ball being placed on the diagram at 1-second intervals. The numbers have been chosen so the motion diagram is always symmetric (the images of the ball on the y-axis on the way up are always the same locations as the images of the ball on the way down), and the time for the entire trip is always an integer number of seconds. (It should be obvious that this will not always happen in reality!) The arrows attached to the ball are the horizontal and vertical components of the velocity. |
| Projectile Motion | 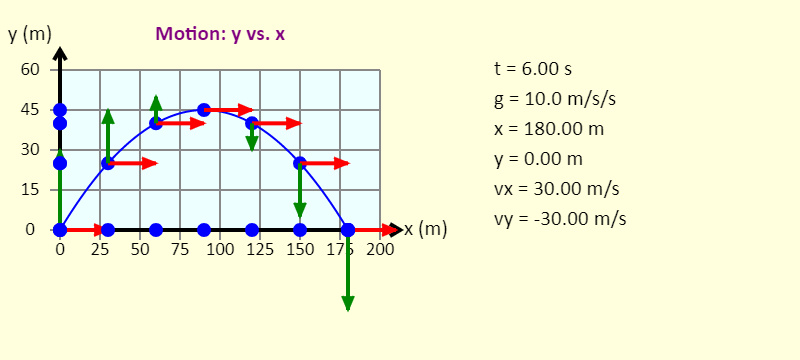 |
The simulation shows a ball experiencing projectile motion. Use the buttons to select different values of g (the acceleration due to gravity), the horizontal component of the initial velocity, and the vertical component of the initial velocity. A motion diagram is drawn, with images of the ball being placed on the diagram at 1-second intervals. The numbers have been chosen so the motion diagram is always symmetric (the images of the ball on the y-axis on the way up are always the same locations as the images of the ball on the way down), and the time for the entire trip is always an integer number of seconds. (It should be obvious that this will not always happen in reality!) The arrows attached to the ball are the horizontal and vertical components of the velocity. |
| Projectile motion - changing the launch angle | 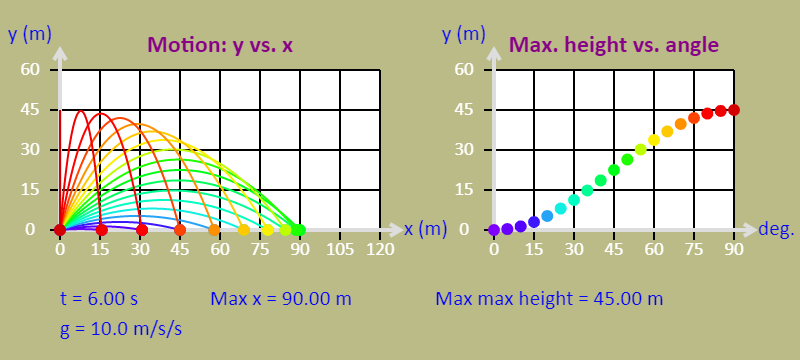 |
The simulation shows balls launched at a range of angles between 0 degrees and 90 degrees to the horizontal, in steps of 5 degrees. There are also as various graphs associated with the motion, so you can see the effect of changing the launch angle. Use the buttons to select different values of g (the acceleration due to gravity), the initial velocity, and what to plot on the vertical axis of the graph (on the right). |
| Monkey and hunter | 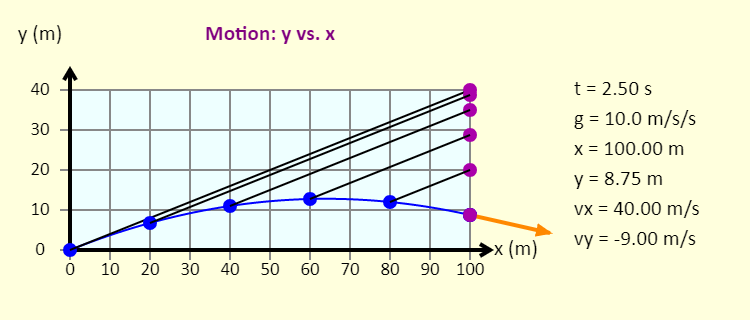 |
The simulation shows the classic physics situation of a monkey and hunter. In this case, the hunter is trying to tranquilize the monkey, so the monkey can be re-located to a better habitat. The monkey is clever - when the tranquilizer dart (in blue) leaves the gun, the monkey (in purple) lets go of the tree branch, and starts to fall straight down. Note that there is a net (not shown) at the bottom to catch the monkey, so the monkey won't get hurt. How should the gun be aimed so the dart hits the monkey? You can explore various parameters, including changing the direction the gun is aimed, changing the value of the acceleration due to gravity, and adjusting the dart's launch speed. |
| Newton's Mountain | 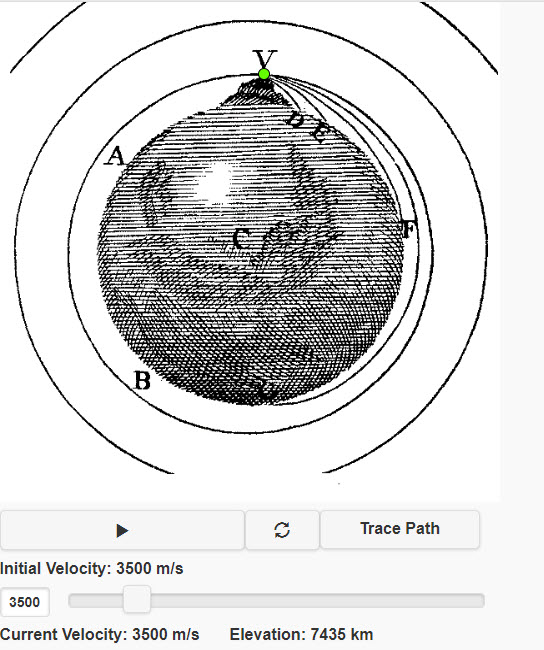 |
The cannon is atop an imaginary mountain far above the atmosphere. (The backdrop diagram is from Sir Isaac's own book, A Treatise of the System of the World, page 5.) For low speeds, the cannonball doesn't get far relative to the Earth's size, and the downward gravity gives a parabolic path. At higher speeds, the cannonball goes far enough that the direction of gravity--always toward the center of the Earth--changes, and so does the shape of the path! |
| Newton's Mountain | 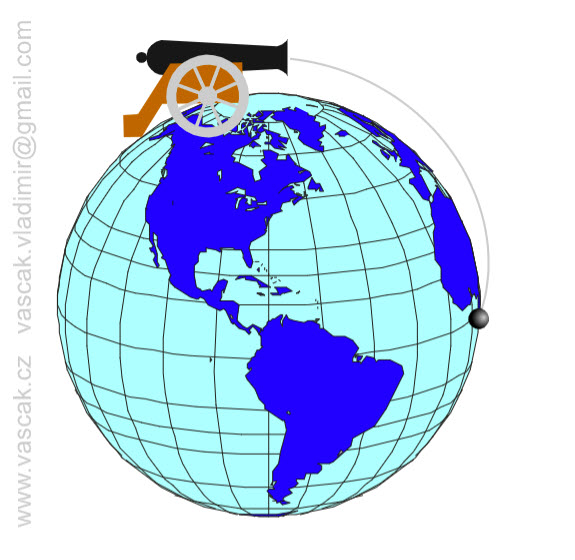 |
Another animation of shooting a cannon ball from on top of a mountain. |