Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations
Student Learning Objectives
Lessons / Lecture Notes
PY106 Notes from Boston University (algebra-based):
Physics 2C notes from Dr. Bobby W.S. Lau (algebra-based)
HyperPhysics (calculus-based)
Important Equations (for algebra-based Physics)
| Davisson-Germer: Electron Diffraction | 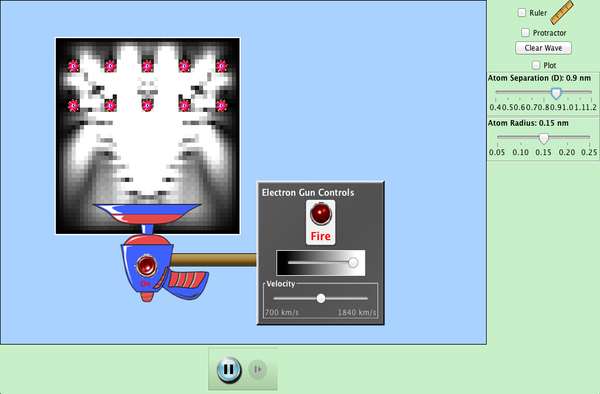 |
Simulate the original experiment that proved that electrons can behave as waves. Watch electrons diffract off a crystal of atoms, interfering with themselves to create peaks and troughs of probability. |
| Stern-Gerlach Experiment | 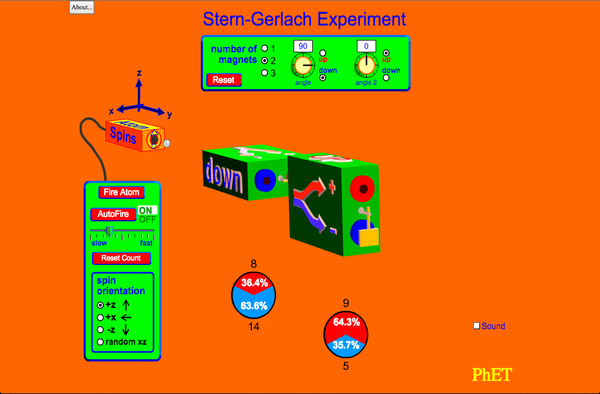 |
The classic Stern-Gerlach Experiment shows that atoms have a property called spin. Spin is a kind of intrinsic angular momentum, which has no classical counterpart. When the z-component of the spin is measured, one always gets one of two values: spin up or spin down. |
| Quantum Wave Interference |
When do photons, electrons, and atoms behave like particles and when do they behave like waves? Watch waves spread out and interfere as they pass through a double slit, then get detected on a screen as tiny dots. Use quantum detectors to explore how measurements change the waves and the patterns they produce on the screen. |
|
| Quantum Bound States | 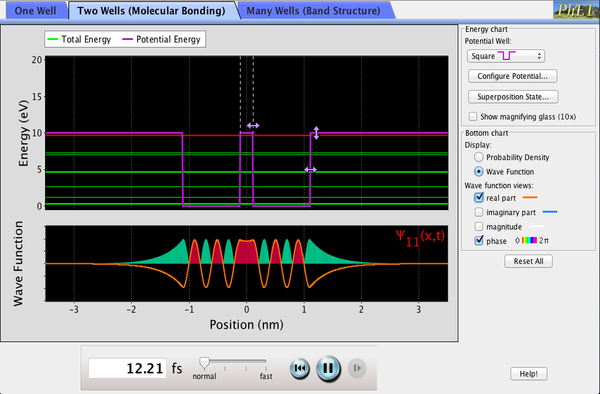 |
Explore the properties of quantum "particles" bound in potential wells. See how the wave functions and probability densities that describe them evolve (or don't evolve) over time. |
| Quantum Tunneling and Wave Packets | 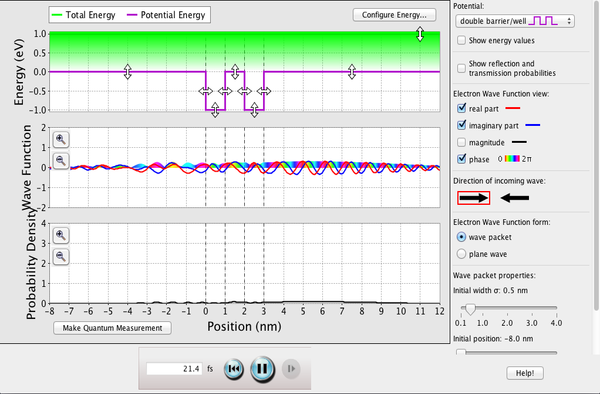 |
Watch quantum "particles" tunnel through barriers. Explore the properties of the wave functions that describe these particles. |
| Quantum Mechanics: 1D Particle States | 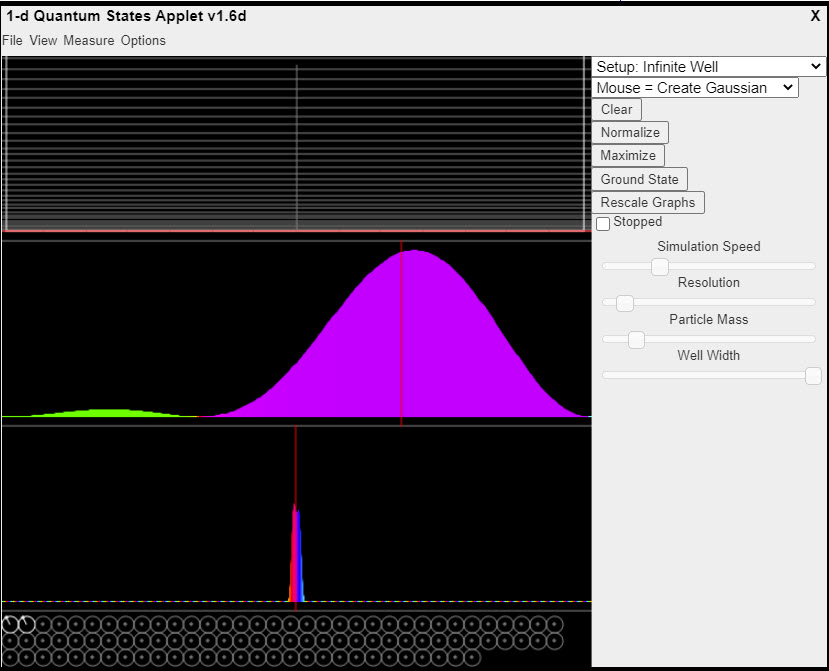 |
This java applet is a quantum mechanics simulation that shows the behavior of a single particle in bound states in one dimension. It solves the Schrödinger equation and allows you to visualize the solutions. At the top of the applet you will see a graph of the potential, along with horizontal lines showing the energy levels. By default it is an infinite square well (zero everywhere inside, infinite at the edges). Below that you will see the probability distribution of the particle's position, oscillating back and forth in a combination of two states. Below the particle's position you will see a graph of its momentum. At the bottom of the screen is a set of phasors showing the magnitude and phase of the lower-energy states. To view a state, move the mouse over its energy level on the potential graph. To select a single state, click on it. You may also select a single state by picking one of the phasors at the bottom and double-clicking on it. Or, you may click on the phasor and drag its value to modify the magnitude and phase. In this way, you can create a combination of states. You may select a different potential from the Setup menu at the top right. |
| Hydrogen Atom Wave Functions | 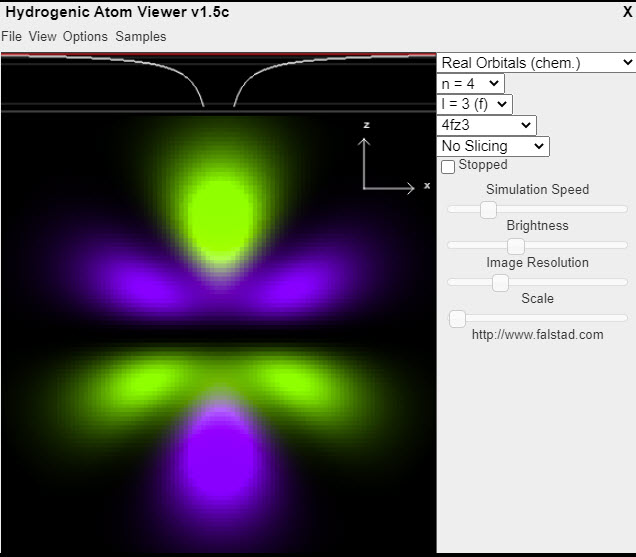 |
This applet displays the wave functions (orbitals) of the hydrogen atom (actually the hydrogenic atom) in 3-D. Select the wavefunction using the popup menus at the upper right. Click and drag the mouse to rotate the view. This applet displays real orbitals (as typically used in chemistry) by default; to display complex orbitals (as typically used in physics) select "Complex Orbitals" from the popup menu in the top upper right. You can also view combinations of orbitals. |
| Models of the Hydrogen Atom | 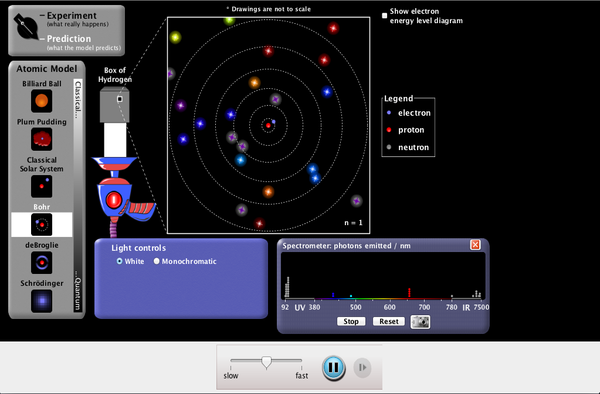 |
How did scientists figure out the structure of atoms without looking at them? Try out different models by shooting light at the atom. Check how the prediction of the model matches the experimental results. |
| Bohr's Theory of the Hydrogen Atom | 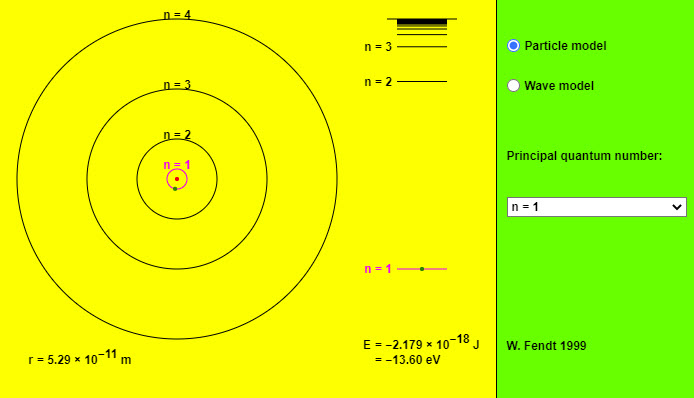 |
This app illustrates a hydrogen atom according to particle or wave model. You can choose a principal quantum number n. The right part of the graphics represents the energy levels of the atom. Right down at the bottom you can read off the orbital radius r and the total energy E. If you try to vary the orbit's radius with pressed mouse button, this will generally lead to a non-stationary state. You can realize that by using the option "Wave model": The green wavy line which symbolizes the de Broglie wave will not be closed in most cases. Only if the circle's circumference is an integer multiple of the wavelength (blue), you will get a stationary state. |
| Bohr Model | 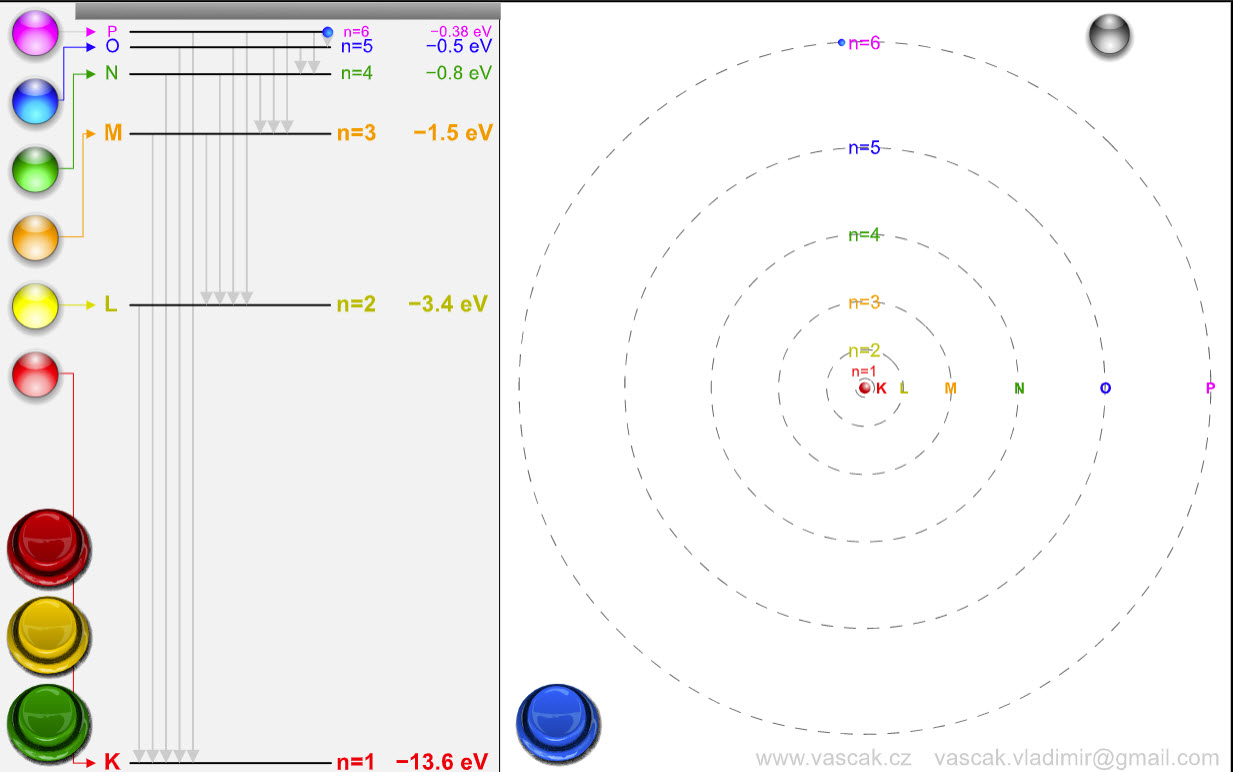 |
A very cool animation showing the Bohr model and transitions between energy levels. |
| Emission Spectra | 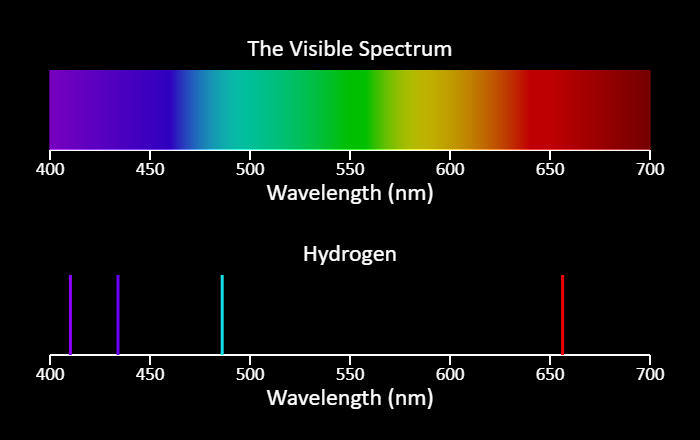 |
This is a simulation of the light emitted by excited gas atoms of particular elements. In some sense, these are atomic fingerprints. Note that the lines shown are the brightest lines in a spectrum - you may be able to see additional lines if you look at the spectrum from a real gas tube. In addition, the observed color could be a bit different from what is shown here. The visible spectrum is always shown as a reference. |
| Build an Atom | 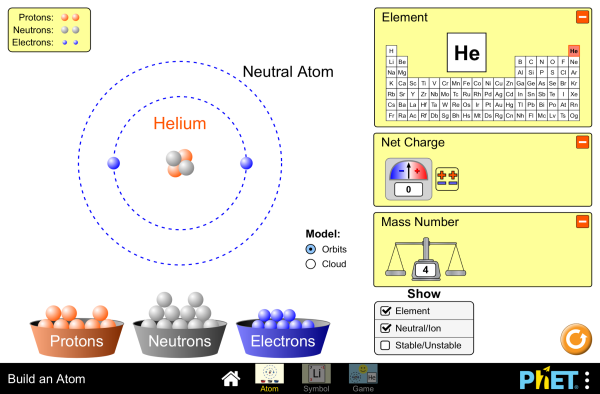 |
Build an atom out of protons, neutrons, and electrons, and see how the element, charge, and mass change. Then play a game to test your ideas! |
| Atomic Interactions | 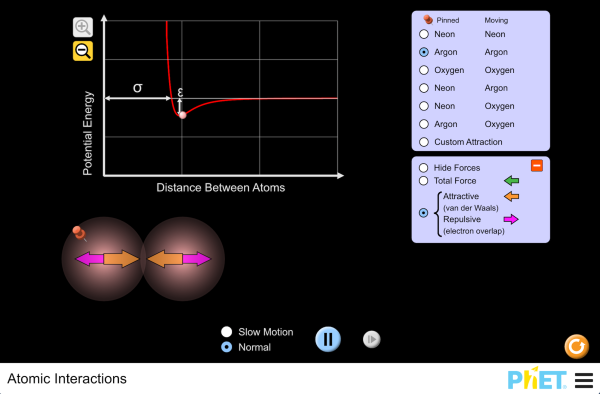 |
Explore the interactions between various combinations of two atoms. Observe the total force acting on the atoms or the individual attractive and repulsive forces. Customize the attraction to see how changing the atomic diameter and interaction strength affects the interaction. |
| Band Structure |
Explore the origin of energy bands in crystals of atoms. The structure of these bands determines how materials conduct electricity. |
|
| Semiconductors |
Dope the semiconductor to create a diode. Watch the electrons change position and energy. |
|
| Molecules and Light |
Turn light source on to explore. Observe what happens in the observation window as you set up different combinations of light source and molecule. Note this simulation is the first to support our zoom and magnification feature, so zoom in for a closer look, if you need to. |
|
| Simplified MRI | 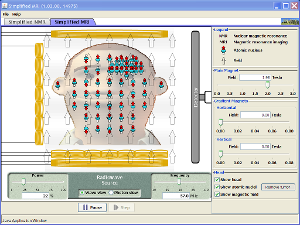 |
Is it a tumor? Magnetic Resonance Imaging (MRI) can tell. Your head is full of tiny radio transmitters (the nuclear spins of the hydrogen nuclei of your water molecules). In an MRI unit, these little radios can be made to broadcast their positions, giving a detailed picture of the inside of your head. |
| Lasers | 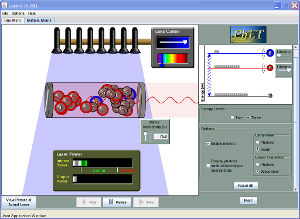 |
Create a laser by pumping the chamber with a photon beam. Manage the energy states of the laser's atoms to control its output. |
| Neon Lights & Other Discharge Lamps | 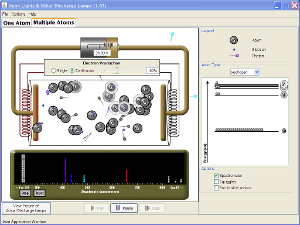 |
Produce light by bombarding atoms with electrons. See how the characteristic spectra of different elements are produced, and configure your own element's energy states to produce light of different colors. |