Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations
Student Learning Objectives
Lessons / Lecture Notes
The Physics Classroom (conceptual)
PY105 Notes from Boston University (algebra-based):
Physics 2A notes from Dr. Bobby W.S. Lau (algebra-based)
HyperPhysics (calculus-based)
Important Equations (for algebra-based Physics)
Example Problems
Example Problems for algebra-based physics (from Physics 10th Edition by Cutnell and Johnson):
Example Problems (Uniform Circular Motion)
Solutions to Example Problems (Uniform Circular Motion)
Example Problems for calculus-based physics (from Physics for Scientists and Engineers 4th Edition by Knight):
Example Problems (Dynamics II)
Solutions to Example Problems (Dynamics II)
| Ladybug Motion 2D | 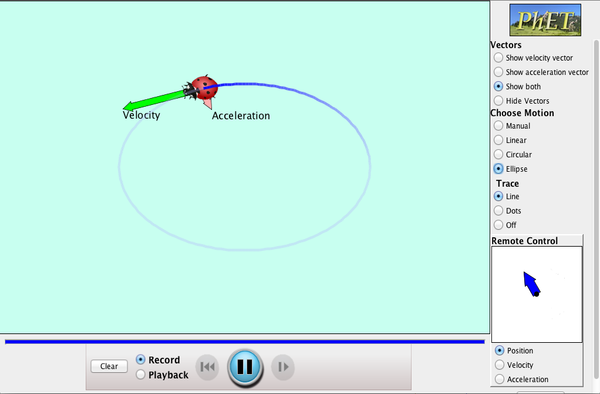 |
Learn about position, velocity and acceleration vectors. Move the ladybug by setting the position, velocity or acceleration, and see how the vectors change. Choose linear, circular or elliptical motion, and record and playback the motion to analyze the behavior. |
| Motion in 2D | 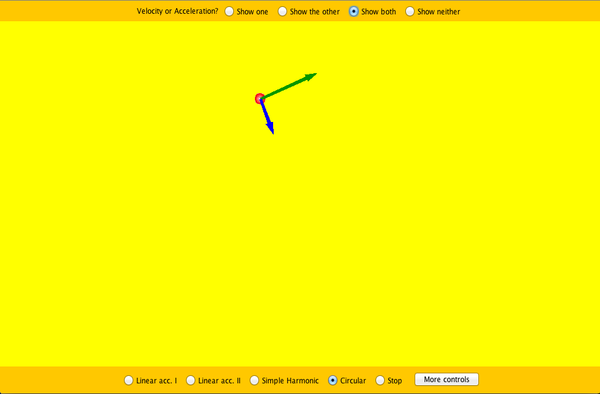 |
Try the new "Ladybug Motion 2D" simulation for the latest updated version. Learn about position, velocity, and acceleration vectors. Move the ball with the mouse or let the simulation move the ball in four types of motion (2 types of linear, simple harmonic, circle). |
| Ladybug Revolution | 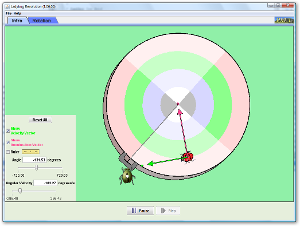 |
Join the ladybug in an exploration of rotational motion. Rotate the merry-go-round to change its angle, or choose a constant angular velocity or angular acceleration. Explore how circular motion relates to the bug's x,y position, velocity, and acceleration using vectors or graphs. |
| Uniform Circular Motion | 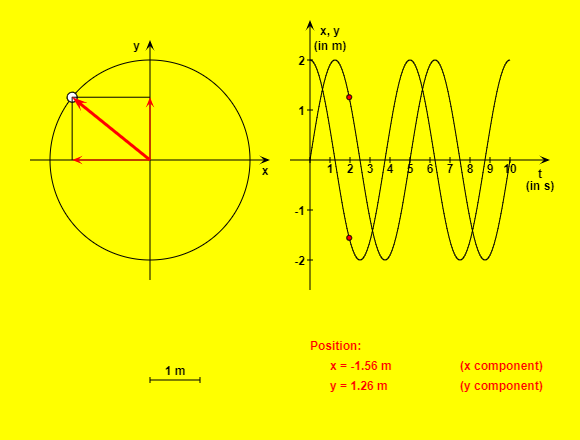 |
This HTML5 app simulates such a circular motion and demonstrates how position, velocity, acceleration and acting force vary in time. The "Reset" button brings the rotating body in its initial position. You can start or stop and continue the simulation with the other button. If you choose the option "Slow motion", the movement will be ten times slower. You can adjust radius, period and mass by using the corresponding input fields. The radio buttons give the possibility to select one of four physical sizes. |
| Uniform Circular Motion | 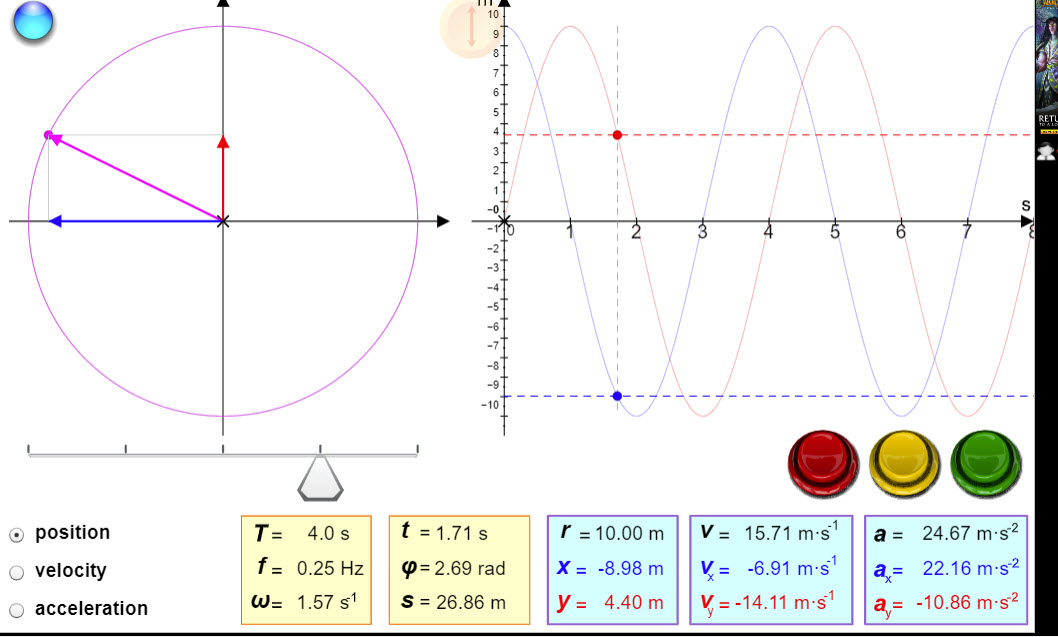 |
This simulation plots the position, velocity, and acceleration of an object moving in uniform circular motion. |
| Uniform Circular Motion |
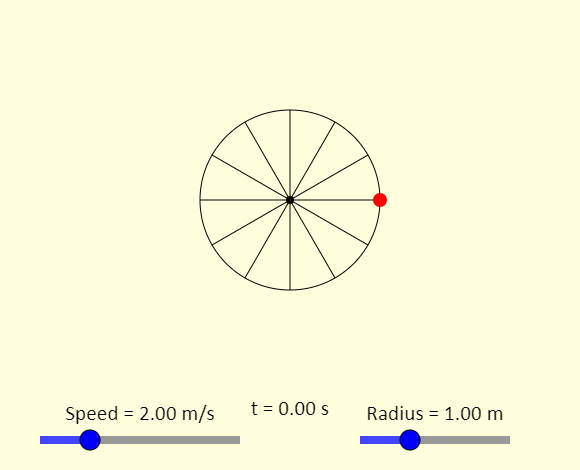 |
This is a simulation of a ball experiencing uniform circular motion, which means it travels in a circle at constant speed. Use the sliders to adjust the speed and the radius of the path. If you show the vectors, you will see the ball's velocity vector, in blue, and its acceleration vector, in green. The velocity vector is always tangent to the circle, and the acceleration vector always points toward the center of the circle.http://physics.bu.edu/~duffy/HTML5/circular_motion.html |
| Disk on a Turntable | 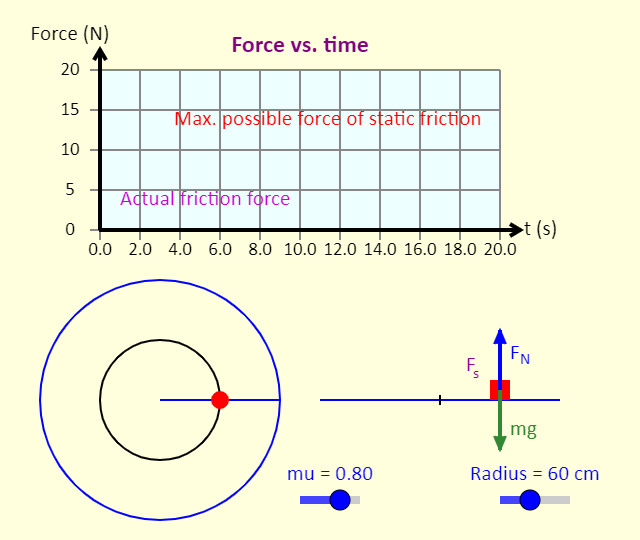 |
This is a simulation of a disk on a turntable. The turntable starts from rest, and then experiences a uniform angular acceleration. The disk on the turntable keeps up with the turntable for a while, but then slides off the turntable. Note that the disk's motion after it starts to slide is something of an approximation. How does the radius (the distance of the disk from the center of the turntable) and the coefficient of static friction (mu) affect when the disk begins to slide on the turntable. Why does the graph of the actual force of friction have the shape it does? What determines the value of the maximum possible force of static friction? |
| Banked Turn |
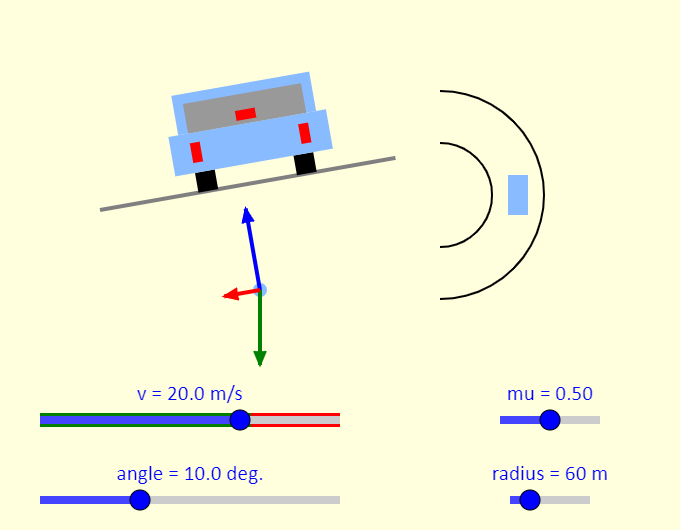 |
The simulation shows a car going around a banked turn. The car is, we hope, experiencing uniform circular motion, moving in a horizontal circle. In the simulation, you see the rear view of the car, an overhead view of the car, as well as the car's free-body diagram. Using the sliders, you can investigate under what conditions the car can safely get around the turn. As you adjust the sliders, you will notice the background behind the speed slider changing. Green shows the speeds at which the car can safely go around the curve, while red shows the speeds at which the car will slip. If slipping happens, a red arrow showing whether the car slides toward the outside or the inside of the curve will appear on both views of the car. |