Student Learning Objectives
Lessons / Lecture Notes
Important Equations
Example Problems
Applets and Animations
Student Learning Objectives
Lessons / Lecture Notes
PY105 Notes from Boston University (algebra-based):
Physics 2C notes from Dr. Bobby W.S. Lau (algebra-based)
HyperPhysics (calculus-based)
Physics 4C notes from Dr. Bobby W.S. Lau (calculus-based)
Important Equations (for algebra-based Physics)
Example Problems
Example Problems for algebra-based physics (from College Physics 2nd Edition by Knight, Jones, and Field):
Example Problems (Oscillations)
Solutions to Example Problems (Oscillations)
Example Problems for calculus-based physics (from Physics for Scientists and Engineers 4th Edition by Knight):
Example Problems (Oscillations)
Solutions to Example Problems (Oscillations)
| Types of Oscillations |  |
This simple animation shows different types of oscillating systems. |
| Masses and Springs: Basics | 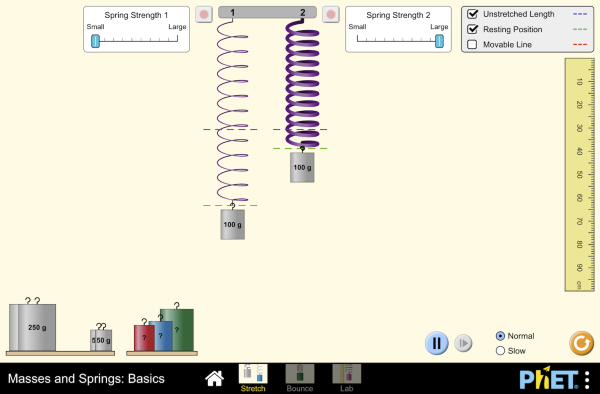 |
Hang masses from springs and discover how they stretch and oscillate. Compare two mass-spring systems, and experiment with spring constant. Transport the lab to different planets, slow down time, and observe the velocity and acceleration throughout the oscillation. |
| Masses and Springs | 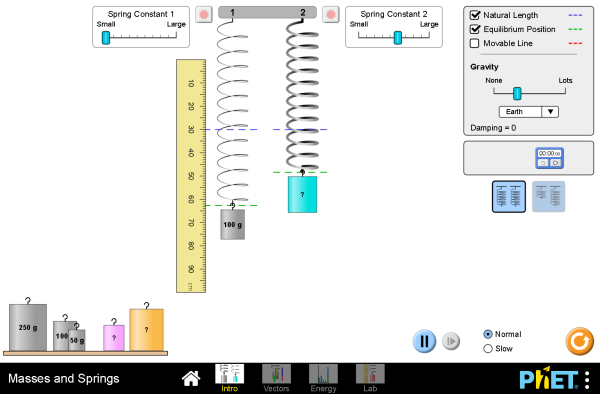 |
Hang masses from springs and adjust the spring constant and damping. Transport the lab to different planets, or slow down time. Observe the forces and energy in the system in real-time, and measure the period using the stopwatch. |
| Hooke's Law | 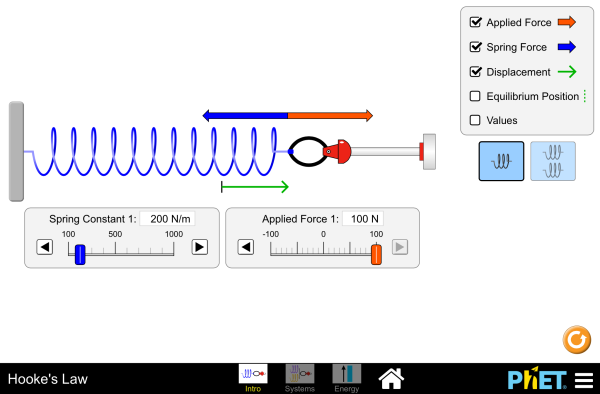 |
Stretch and compress springs to explore the relationships between force, spring constant, displacement, and potential energy! Investigate what happens when two springs are connected in series and parallel. |
| Pendulum Lab | 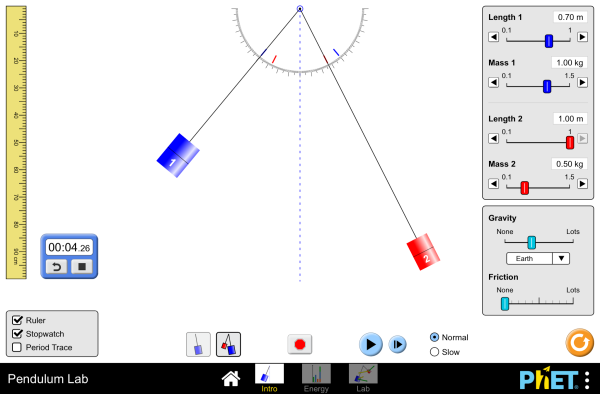 |
Play with one or two pendulums and discover how the period of a simple pendulum depends on the length of the string, the mass of the pendulum bob, the strength of gravity, and the amplitude of the swing. Observe the energy in the system in real-time, and vary the amount of friction. Measure the period using the stopwatch or period timer. Use the pendulum to find the value of g on Planet X. Notice the anharmonic behavior at large amplitude. |
| Spring Pendulum |
This HTML5 app demonstrates the variation of elongation, velocity, acceleration, force and energy during the oscillation of a spring pendulum (assumed with no friction). The "Reset" button brings the body of pendulum to its initial position. You can start or stop and continue the simulation with the other button. If you choose the option "Slow motion", the movement will be ten times slower. The spring constant, the mass, the gravitational acceleration and the amplitude of the oscillation can be changed within certain limits. In order to select another physical size you have to click on the appropriate one of the five radio buttons. |
|
| Position vs. Time |
This applet shows a graph of position vs. time for a spring-mass system. |
|
| Energy vs. Time | 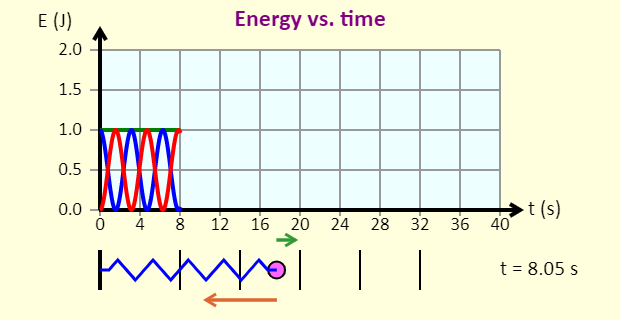 |
This applet allows you to graph energy vs time, energy vs. position, speed vs. position, and velocity vs. position for a spring-mass system. |
| Spring Mass Oscillations | The animation shows oscillations of a mass attached to a spring. It is very instructive to study the graphs when the damping coefficient is not equal to zero. | |
| Position vs. Time (with Damping) | 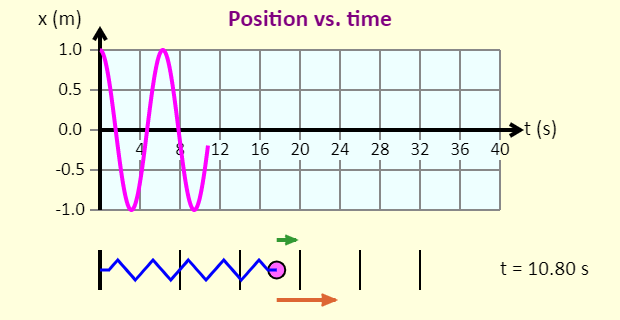 |
This applet shows a graph of position vs. time for a damped spring-mass system. |
| A Simple Pendulum |
This simple applet that allows you to plot angular position vs. time for a simple pendululm. |
|
| A Simple Pendulum (with Damping) | This simple applet that allows you to plot angular position vs. time for a damped simple pendululm. | |
| SHM and Uniform Circular Motion |
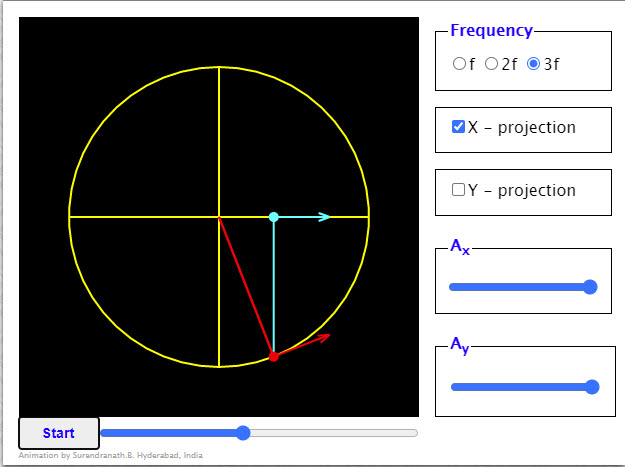 |
The red particle is going round the circular path in anti-clock wise sense (considered positive) with a uniform speed and its x-projection and y - projection are shown in cyan and orange respectively. |
| Forced Damped Oscillations | 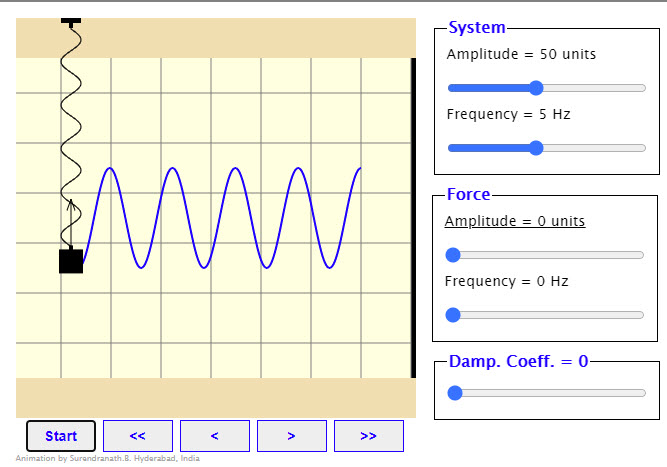 |
Oscillating body is initially at the top extreme position. The amplitude and the frequency of oscillations can be adjusted using the sliders. The black vector is the force on the body due to the spring. A periodic force whose frequency and amplitude can be varied can be applied on the body. This force vector is shown in green color. A resistive force can also be made to act on the body. This is shown in red color. This force too can be varied by adjusting the damping coefficient slider. |
| SHM and Uniform Circular Motion | 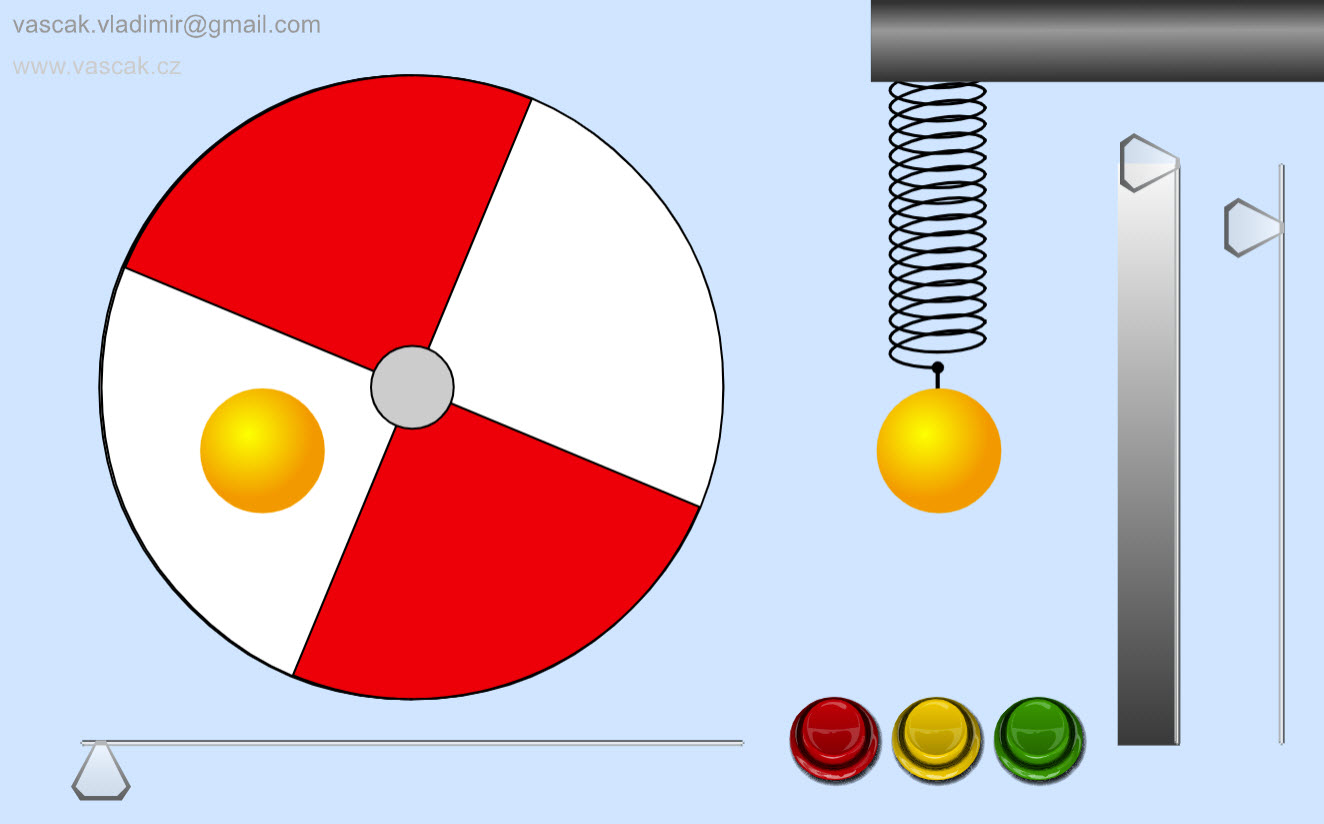 |
This animation shows the connection between SHM and uniform circular motion. |
| SHM and Uniform Circular Motion | 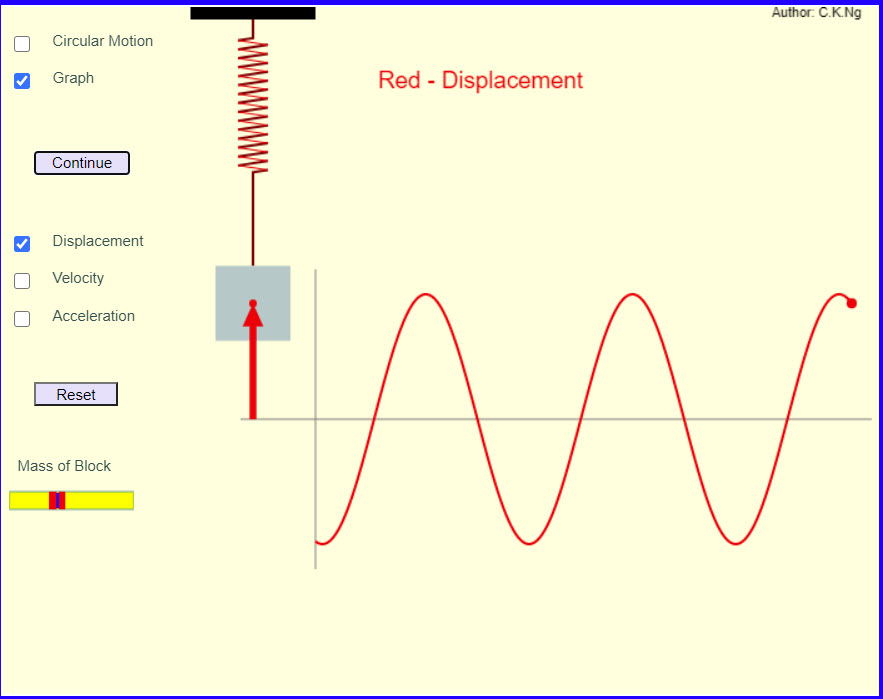 |
Outstanding applet showing the connection between SHM and uniform circular motion. |
| SHM and Uniform Circular Motion | 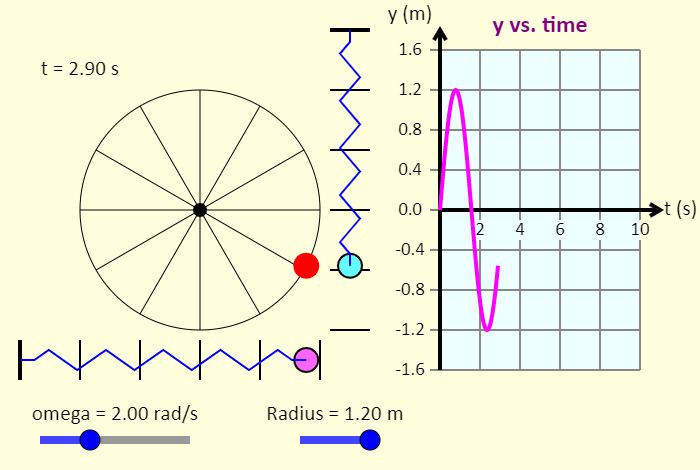 |
This simulation compares the motion of a ball experiencing uniform circular motion to two different simple harmonic motions, one vertical and one horizontal. The point of the simulation is to show that the horizontal motion of the ball exactly matches that of the ball attached to the horizontal spring, and that the vertical motion of the ball exactly matches that of the ball attached to the vertical spring. The graph also shows that the position versus time graphs of these motions are sinusoidal. |
| Phase of SHM | 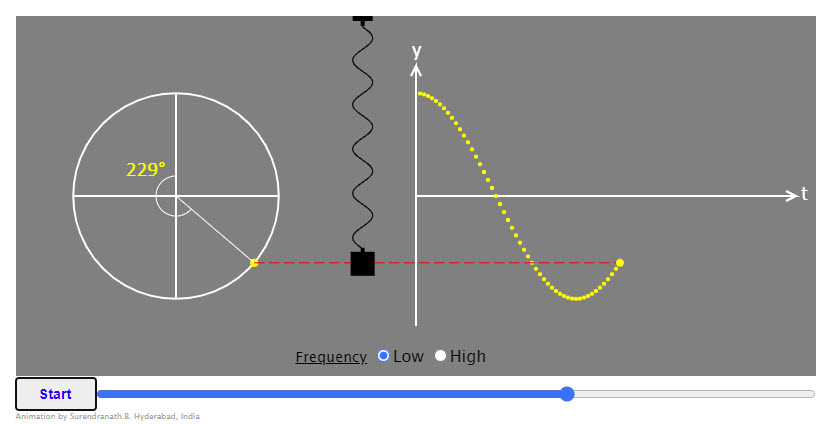 |
Nice animation showing the phase of a spring-mass system. |
| Harmonics |
This nice animatiuon shows the response of a spring-mass system to different kinds of external forces. |